XI IPS 2
27
1. logika matematika
Dalam logika matematika, kita belajar untuk mementukan nilai dari suatu pernyataan, baik bernilai benar atau salah. Pernyataan sendiri terbagi menjadi 2 jenis, yaitu:
- Pernyataan tertutup (kalimat tertutup)
Pernyataan tertutup atau kalimat tertutup adalah suatu pernyataan yang sudah memiliki nilai benar atau salah.
Contoh:
“5 adalah bilangan genap”, kalimat tersebut bernilai salah karena yang benar adalah “5 adalah bilangan ganjil”.
“5 adalah bilangan genap”, kalimat tersebut bernilai salah karena yang benar adalah “5 adalah bilangan ganjil”.
- Pernyataan terbuka (kalimat terbuka)
Pernyataan terbuka atau kalimat terbuka adalah suatu pernyataan yang belum dapat ditentukan nilai kebenarannya karena adanya suatu perubah atau variabel.
Contoh logika matematika:

Saat 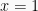 , maka
, maka 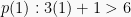 bernilai salah
bernilai salah
Saat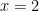 , maka
, maka 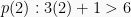 bernilai benar
bernilai benar
Saat
Ingkaran atau Negasi dari suatu Pernyataan
Ingkaran atau negasi adalah kebalikan nilai dari suatu pernyataan, dimana ketika suatu pernyataan bernilai benar, maka negasinya bernilai salah dan saat suatu pernyataan bernilai salah, negasinya bernilai benar. Ingkaran atau negasi dari pernyataan 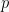 dilambangkan dengan
dilambangkan dengan 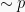 .
.
Pernyataan Kuantor
Pernyataan kuantor adalah bentuk logika matematika berupa pernyataan yang memiliki kuantitas. Dalam pernyataan kuantor, pada umumnya terdapat kata semua, seluruh, setiap, beberapa, ada, dan sebagian.
Kata-kata yang senilai dengan seluruh, semua, setiap termasuk dalam kuantor universal dan kata-kata yang senilai dengan sebagian, beberapa, ada termasuk dalam kuantor eksistensial. Kuantor universal dan kuantor eksistensial saling beringkaran.
Pernyataan Majemuk, Bentuk Ekuivalen dan Ingkarannya
Dalam logika matematika, beberapa pernyataan dapat dibentuk menjadi satu pernyataan dengan menggunakan kata penghubung logika seperti dan, atau, maka dan jika dan hanya jika. Pernyataan gabungan tersebut disebut dengan pernyataan majemuk.
Dalam logika matematika, kata hubung tersebur masing-masing memiliki lambang dan istilah sendiri.

Tabel Kebenaran Konjungsi

Dari tabel diatas dapat disimpulkan bahwa sifat dari konjungsi adalah bernilai benar jika kedua pernyataan penyusun dari peryataan majemuk keduanya bernilai benar.
- Konjungsi (∧)
Suatu pernyataan p dan q dapat digabungkan dengan menggunakan kata hubung ‘dan’ sehingga membentuk pernyataan majemuk ‘p dan q’ yang disebut konjungsi yang dilambangkan dengan “p∧q”. Berikut adalah tabel kebenaran konjungsi.
| p | q | p∧q |
| B | B | B |
| B | S | S |
| S | B | S |
| S | S | S |
Dari tabel diatas dapat disimpulkan bahwa dalam konsep konjungsi akan bernilai benar jika dan hanya jika kedua pernyataan (p dan q) benar
Contoh:
Budi sudah makan belajar dan makan
Misalkan, untuk dapat diizinkan bermain oleh Ibu, Budi harus memenuhi kondisi di atas. Jika satu saja atau bahkan kedua pernyataan tersebut dilanggar, maka Budi tidak diizinkan untuk bermain.
Konjungsi adalah pernyataan majemuk dengan kata hubung “dan”. Sehingga, notasi “p^q” dibaca “p dan q”.
Tabel nilai kebenaran konjungsi:

Dari tabel di atas, kita dapat melihat bahwa konjungsi hanya akan benar jika kedua pernyataan (p dan q) benar.
Contoh:
- p: 3 adalah bilangan prima (pernyataan bernilai benar)
- q: 3 adalah bilangan ganjil (pernyataan bernilai benar)
- p^q: 3 adalah bilangan prima dan ganjil (pernyataan bernilai benar)
Tabel Kebenaran Disjungsi

Dari tabel diatas dapat disimpulkan bahwa sifat dari disjungsi adalah bernilai salah jika kedua pernyataan penyusun dari peryataan majemuk keduanya bernilai salah.
- Disjungsi
Suatu pernyataan p dan q dapat digabungkan dengan menggunakan kata hubung ‘atau’ sehingga membentuk pernyataan majemuk ‘p atau q’ yang disebut disjungsi yang dilambangkan dengan “p ∨ q”. Berikut adalah tabel kebenaran disjungsi.
| p | q | p∨q |
| B | B | B |
| B | S | B |
| S | B | B |
| S | S | S |
Dari tabel diatas dapat disimpulkan bahwa dalam konsep disjungsi hanya akan bernilai salah jika kedua pernyataan (p dan q) salah.
Contoh:
Bandung atau Palembang adalah kota yang terletak di Pulau Jawa
Pernyataan Bandung adalah kota yang terletak di Pulau Jawa adalah benar. Pernyataan Palembang adalah kota yang terletak di Pulau Jawa adalah salah. Sehingga pernyataan Bandung atau Palembang adalah kota yang terletak di Pulau Jawa bernilai benar.
Tabel Disjungsi (V)
Disjungsi adalah pernyataan majemuk dengan kata hubung “atau”. Sehingga notasi “pVq” dibaca “p atau q”.
Tabel nilai kebenaran disjungsi:

Jika kita lihat pada tabel kebenaran, disjungsi hanya salah jika kedua pernyataan (p dan q) salah.
Contoh:
- p: Paus adalah mamalia (pernyataan bernilai benar)
- q: Paus adalah herbivora (pernyataan bernilai salah)
- pVq: Paus adalah mamalia atau herbivora (pernyataan bernilai benar)
Kebenaran Implikasi

Pada sifat implikasi ini, 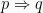 , p disebut sebagai hipotesa dan q sebagai konklusi. Pada implikasi ini akan bernilai salah ketika konklusi salah dan hipotesa benar.
, p disebut sebagai hipotesa dan q sebagai konklusi. Pada implikasi ini akan bernilai salah ketika konklusi salah dan hipotesa benar.
- mplikasi (⟹)
Implikasi bisa dipandang sebagai hubungan antara dua pernyataan di mana pernyataan kedua merupakan konsekuensi logis dari pernyataan pertama. Implikasi ditandai dengan notasi ‘⟹’. Misalkan p, q adalah pernyataan, implikasi berikut
p ⟹ q
dibaca ‘jika p maka q’. Berikut adalah tabel kebenaran disjungsi.
| p | q | p⇒q |
| B | B | B |
| B | S | S |
| S | B | B |
| S | S | B |
Dari tabel diatas dapat disimpulkan bahwa dalam konsep implikasi akan bernilai salah jika dan hanya jika sebab bernilai benar namun akibat bernilai salah. Selain itu implikasi bernilai benar.
Contoh:
Jika Budi sembuh maka Budi akan sekolah
Jika betul Budi sembuh lalu Budi masuk sekolah, Budi telah melakukan hal yang benar. Namun jika Budi sembuh namun dia tidak masuk sekolah, Budi telah berbuat salah karena mengingkari janjinya. Lalu, bagaimana jika Budi belum sembuh? Perhatikan bahwa Budi hanya berjanji masuk sekolah jika dia sembuh. Akibatnya jika dia masih belum sembuh, tidak masalah bagi Budi untuk masuk sekolah ataupun tidak karena dia tidak melanggar janjinya.
Implikasi adalah pernyataan majemuk dengan kata hubung “jika… maka…” Sehingga notasi dari “p->q” dibaca “Jika p, maka q”. Adapun tabel nilai kebenaran dari implikasi:

Dari tabel terlihat bahwa implikasi hanya bernilai salah jika anteseden (p) benar, dan konsekuen (q) salah.
Contoh:
- p: Andi belajar dengan aplikasi ruangguru. (pernyataan bernilai benar)
- q: Andi dapat belajar di mana saja. (pernyataan bernilai benar)
- p->q: Jika Andi belajar dengan aplikasi ruangguru, maka Andi dapat belajar di mana saja (pernyataan bernilai benar)
Tabel Kebenaran Biimplikasi

Pada sifat biimplikasi, penyataan majemuk akan bernilai benar jika kedua pernyataan penyusunnya bernilai sama, keduanya benar atau keduanya salah.
- Biimplikasi
Suatu pernyataan p dan q dapat digabungkan dengan menggunakan kata hubung ‘jika dan hanya jika’ sehingga membentuk pernyataan majemuk ‘p jika dan hanya jika q’ yang disebut biimplikasi yang dilambangkan dengan “p ⇔ q”. Berikut adalah tabel kebenaran biimplikasi:
| p | q | p⇔q |
| B | B | B |
| B | S | S |
| S | B | S |
| S | S | B |
Dari tabel diatas dapat disimpulkan bahwa dalam konsep biimplikasi akan bernilai benar jika sebab dan akibatnya (pernyataan p dan q) bernilai sama. Baik itu sama-sama benar, atau sama-sama salah.
Contoh:
Ayah mendapatkan gaji jika dan hanya jika ayah bekerja
Jika ayah mendapatkan gaji maka ayah bekerja dan jika ayah telah bekerja maka ayah akan mendapat gaji. Sebalinya, jika ayah tidak mendapatkan gaji maka ayah sedang tidak bekerja dan jika ayah tidak bekerja maka ayah tidak akan mendapat gaji.
Biimplikasi (<->)
Biimplikasi adalah pernyataan majemuk dengan kata hubung “… jika dan hanya jika”. Sehingga, notasi dari “p<-> q” akan dibaca “p jika dan hanya jika q”.
Tabel nilai kebenaran Biimplikasi:

Dari tabel kebenaran tersebut, dapat kita amati bahwa biimplikasi akan bernilai benar jika sebab dan akibatnya (pernyataan p dan q) bernilai sama. Baik itu sama-sama benar, atau sama-sama salah.
Contoh:
- p: 30 x 2 = 60 (pernyataan bernilai benar)
- q: 60 adalah bilangan ganjil (pernyataan bernilai salah)
- p<->q: 30 x 2 = 60 jika dan hanya jika 60 adalah bilangan ganjil (pernyataan bernilai salah).
Tautologi dan Kontradiksi
Tautologi adalah pernyataan majemuk yang selalu benar untuk semua kemungkinan yang ada dan kontradiksi adalah kebalikannya, yaitu pernyataan majemuk yang bernilai salah untuk semua kemungkinan yang ada.
Bentuk Ekuivalen Pernyataan Majemuk
Pernyataan majemuk yang memiliki nilai sama untuk semau kemungkinannya dikatakan ekuivalen. Notasi ekuivalen dalam logika matematika adalah “ “.
“.
Bentuk-bentuk pernyataan yang saling ekuivalen adalah:

Ingkaran Pernyataan Majemuk
Ingkaran Konjungsi: 
Ingkaran Disjungsi: 
Ingkaran Implikasi: 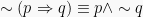
Ingkaran Biimplikasi: 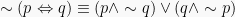
Konvers, Invers dan Kontraposisi
Konvers, invers dan kontraposisi adalah bentuk lain dari implikasi, dimana:
Konvers dari 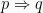 adalah
adalah 
Invers dari 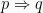 adalah
adalah 
Kontraposisi dari 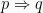 adalah
adalah 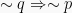
Penarikan Kesimpulan (Logika Matematika)
Penarikan kesimpulan adalah konklusi dari beberapa pernyataan majemuk (premis) yang saling terkait. Dalam penarikan kesimpulan terdiri dari beberapa cara, yaitu:

Contoh Soal Logika Matematika:
Soal 1:
Premis 1 : Jika Andi rajin belajar, maka Andi juara kelas
Premis 2 : Andi rajin belajar
Kesimpulan dari kedua premis diatas adalah ….
Premis 1 : Jika Andi rajin belajar, maka Andi juara kelas
Premis 2 : Andi rajin belajar
Kesimpulan dari kedua premis diatas adalah ….
Jawab:
Premis 1 :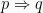
Premis 2 : p
Kesimpulan : q (modus ponens)
Jadi kesimpulannya adalah Andi juara kelas.
Premis 1 :
Premis 2 : p
Kesimpulan : q (modus ponens)
Jadi kesimpulannya adalah Andi juara kelas.
Soal 2:
Premis 1 : Jika hari hujan, maka sekolah libur
Premis 2 : sekolah tidak libur
Kesimpulan dari kedua premis diatas adalah ….
Premis 1 : Jika hari hujan, maka sekolah libur
Premis 2 : sekolah tidak libur
Kesimpulan dari kedua premis diatas adalah ….
Jawab:
Premis 1 :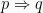
Premis 2 :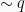
Kesimpulan : (modus tollens)
Jadi kesimpulannya adalah hari tidak hujan.
Premis 1 :
Premis 2 :
Kesimpulan : (modus tollens)
Jadi kesimpulannya adalah hari tidak hujan.
Soal logika matematika 3:
Premis 1 : Jika Ani nakal, maka Ibu marah
Premis 2 : Jika Ibu marah, maka Ani tidak dapat uang saku
Kesimpulan dari kedua premis diatas adalah …
Premis 1 : Jika Ani nakal, maka Ibu marah
Premis 2 : Jika Ibu marah, maka Ani tidak dapat uang saku
Kesimpulan dari kedua premis diatas adalah …
Jawab:
Premis 1 :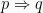
Premis 2 :
Kesimpulan : (silogisme)
(silogisme)
Jadi kesimpulannya adalah Jika Ani nakal, maka Ani tidak dapat uang saku.
Premis 1 :
Premis 2 :
Kesimpulan :
Jadi kesimpulannya adalah Jika Ani nakal, maka Ani tidak dapat uang saku.
a. p ∨ ~p
p ∨ ~ p
T T F T
F T T F
b. ~[(~p ⇒ r) ∨ (p ⇒ ~q)] ∧ r
~ [(~ p ⇒ r) ∨ (p ⇒ ~ q)] ∧ r
F F T T T T T F F T F T
F F T T F T T F F T F F
F F T T T T T T T F F T
F F T T F T T T T F F F
F T F T T T F T F T F T
F T F F F T F T F T F F
F T F T T T F T T F F T
F T F F F T F T T F F F
B. Ekuivalen secara logika
Dua proposisi dikatakan ekuivalen secara logika jika nilai kebenaran dari
kedua pernyataan tersebut sama. Lambang untuk ekuivalen adalah “ ≡ ”
Sebagai contoh, perhatikan tabel kebenaran dari proposisi (p ⇔ q) dan (p ⇒
q) ∧ (q ⇒ p) berikut.
p ⇔ q (p ⇒ q) ∧ (q ⇒ p)
T T T T T T T T T T
T F F T F F F F T T
F F T F T T F T F F
F T F F T F T F T F
Karena nilai kebenaran dari kedua proposisi diatas sama (berdasar tabel
kebenaran), maka
(p ⇔ q) ≡ (p ⇒ q) ∧ (q ⇒ p).
Beberapa hukum ekuivalensi logika disajikan dalam daftar dibawah ini:
1. Hukum Komutatif
a. p ∧ q ≡ q ∧ p
b. p ∨ q ≡ q ∨ p
2. Hukum asosiatif
a. (p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
b. (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
3. Hukum distributive
a. p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
b. p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
4. Hukum identitas
a. p ∧ T ≡ p
b. p ∨ F ≡ p
5. Hukum ikatan
a. p ∧ F ≡ F
b. p ∨ T ≡ T
6. Hukum negasi
a. p ∨ ~p ≡ T
b. p ∧ ~p ≡ F
7. Hukum negasi ganda
~(~p) ≡ p
8. Hukum idempotent
a. p ∧ p ≡ p
b. p ∨ p ≡ p
9. Hukum De Morgan
a. ~(p ∧ q) ≡ ~p ∨ ~q
b. ~(p ∨ q) ≡ ~p ∧ ~q
10. Hukum Penyerapan
a. p ∨ (p ∧ q) ≡ p
b. p ∧ (p ∨ q) ≡ p
11. Negasi T dan F
a. ~T ≡ F
b. ~F ≡ T
C. Konvers, Invers, dan Kontraposisi
Terdapat beberapa implikasi lain yang berkaitan dengan proposisi p ⇒ q, yaitu
proposisi sederhana yang merupakan variasi dari implikasi. Perhatikan
proposisi berikut:
Jika Amir mempunyai mobil, maka ia orang kaya.
Variasi dari proposisi diatas adalah sebagai berikut:
a. Jika Amir orang kaya, maka ia mempunyai mobil.
b. Jika Amir tidak mempunyai mobil, maka ia bukan orang kaya.
c. Jika Amir bukan orang kaya, maka ia tidak mempunyai mobil.
3
Bahan kuliah Logika Matematika
Proposisi (a) disebut konvers, (b) disebut invers, dan (c) disebut kontraposisi.
Tabel berikut ini memperlihatkan tabel kebenaran dari ketiga variasi proposisi
p ⇒ q. Dari tabel tersebut terlihat bahwa proposisi p ⇒ q ekuivalen secara
logika dengan kontraposisinya ~q ⇒ ~p.
p q ~p ~q
Kondisional Konvers Invers Kontraposisi
p ⇒ q q ⇒ p
~p ⇒
~q
~q ⇒ ~p
T T F F T T T T
Latihan
1. Buatlah tabel kebenaran dari proposisi berikut:
a. ~p ∨ (q ∧ ~r)
b. (p ∧ q) ⇔ ~ (r ∨ s)
c. ~ (p ∧ r) ∨ [(~p ∧ ~q) ⇒ r]
2. Periksalah menggunakan tabel kebenaran apakah proposisi berikut merupakan
tautology, kontradiksi atau kontingen.
a. p ∧ [q ∧ (p ∨ q)]
b. (p ⇒ ~q) ⇒ (~q ⇒ p)
c. (r ∧ p) ⇒ [ (q ∧ ~p) ⇒ (~q ⇒ r)]
3. Tentukan konvers, invers, dan kontraposisi dari proposisi berikut dan tentukan
nilai kebenarannya.
a. Jika x, y bilangan asli, maka x – y adalah bilangan asli.
b. Jika x,y bilangan ganjil, maka x2
+ y2
adalah bilangan ganjil.
c. Jika A = ∅, maka n(A) = 0.
4. Tentukan pernyataan kondisional yang mempunyai:
a. Invers p ⇒ ~q
b. Kontraposisi ~p ⇒ q
c. Konvers (p ∨ q) ⇒ ~r
d. Invers (p ∧ ~q) ⇒ ~(r ∧ ~s)
Contoh Soal:
Soal No. 1
Tentukan negasi dari pernyataan-pernyataan berikut:
a) Hari ini Jakarta banjir.
b) Kambing bisa terbang.
c) Didi anak bodoh
d) Siswa-siswi SMANSA memakai baju batik pada hari Rabu.
Pembahasan
a) Tidak benar bahwa hari ini Jakarta banjir.
b) Tidak benar bahwa kambing bisa terbang.
c) Tidak benar bahwa Didi anak bodoh
d) Tidak benar bahwa siswa-siswi SMANSA memakai baju batik pada hari Rabu.
Atau boleh juga dengan format berikut:
a) Hari ini Jakarta tidak banjir.
b) Kambing tidak bisa terbang.
c) Didi bukan anak bodoh
d) Siswa-siswi SMANSA tidak memakai baju batik pada hari Rabu.
Soal No. 2
Tentukan negasi (ingkaran) dari pernyataan-pernyataan berikut:
a) p : Semua dokter memakai baju putih saat bekerja.
b) p : Semua jenis burung bisa terbang
c) p : Semua anak mengikuti ujian fisika hari ini.
Pembahasan
Pernyataan yang memuat kata "Semua" atau "Setiap" negasinya memuat kata "Beberapa" atau "Ada" seperti berikut:
a) ~p : Ada dokter tidak memakai baju putih saat bekerja.
b) ~p : Beberapa jenis burung tidak bisa terbang
c) ~p : Beberapa anak tidak mengikuti ujian fisika hari ini.
Soal No. 3
Ingkaran dari pernyataan “Beberapa bilangan prima adalah bilangan genap” adalah....
A. Semua bilangan prima adalah bilangan genap.
B. Semua bilangan prima bukan bilangan genap.
C. Beberapa bilangan prima bukan bilangan genap.
D. Beberpa bilangan genap bukan bilangan prima.
E. Beberapa bilangan genap adalah bilangan prima.
Pembahasan
p : Beberapa bilangan prima adalah bilangan genap
~p : Semua bilangan prima bukan bilangan genap
Soal No. 4
Tentukan pernyataan majemuk hasil penggabungan pasangan-pasangan pernyataan berikut dengan menggunakan operasi konjungsi (DAN):
a) p : Hari ini Jakarta hujan
q : Hari ini Jakarta banjir
b) p : Iwan memakai topi
q : Iwan memakai dasi
c) p : Mahesa anak jenius.
q : Mahesa anak pemalas.
Pembahasan
a) p : Hari ini Jakarta hujan
q : Hari ini Jakarta banjir
p ∧ q : Hari ini Jakarta hujan dan banjir
b) p : Iwan memakai topi
q : Iwan memakai dasi
p ∧ q : Iwan memakai topi dan dasi
c) p : Mahesa anak jenius.
q : Mahesa anak pemalas.
p ∧ q : Mahesa anak jenius tetapi pemalas
Kata "dan" bisa diganti dengan "tetapi", "walaupun", "meskipun" selaraskan dengan pernyataan.
Soal No. 5
Diberikan dua pernyataan sebagai berikut:
a) p : Hari ini Jakarta hujan lebat.
q : Hari ini aliran listrik putus.
Nyatakan dengan kata-kata:
a) p ∧ q
b) p ∧ ~q
c) ~p ∧ q
d) ~p ∧ ~q
Pembahasan
a) Hari ini Jakarta hujan lebat dan aliran listrik putus
b) Hari ini Jakarta hujan lebat dan aliran listrik tidak putus
c) Hari ini Jakarta tidak hujan lebat dan aliran listrik putus
d) Hari ini Jakarta tidak hujan lebat dan aliran listrik tidak putus
Soal No. 6
Diberikan data:
Pernyataan p bernilai salah
Pernyataan q bernilai benar
Tentukan nilai kebenaran dari konjungsi di bawah ini:
a) p ∧ q
b) p ∧ ~q
c) ~p ∧ q
d) ~p ∧ ~q
Pembahasan
Tabel Nilai kebenaran untuk konjungsi :
p
|
q
|
p ∧ q
|
B
|
B
|
B
|
B
|
S
|
S
|
S
|
B
|
S
|
S
|
S
|
S
|
Terlihat bahwa konjungsi bernilai benar jika kedua pernyataan bernilai benar.
Kita terapkan pada soal salah satunya dengan cara tabel:
p
|
q
|
~p
|
~q
|
p ∧ q
|
p ∧ ~q
|
~p ∧ q
|
~p ∧ ~q
|
S
|
B
|
B
|
S
|
S
|
S
|
B
|
S
|
Dari tabel di atas
a) p ∧ q bernilai salah
b) p ∧ ~q bernilai salah
c) ~p ∧ q bernilai benar
d) ~p ∧ ~q bernilai salah
Soal No. 7
Gabungkan pasangan pernyataan-pernyataan berikut dengan menggunakan operasi disjungsi (ATAU):
a) p : Ibu memasak ayam goreng
q : Ibu membeli soto babat di pasar
b) p : Pak Bambang mengajar matematika
q : Pak Bambang mengajar bahasa inggris
Pembahasan
a) p : Ibu memasak ayam goreng
q : Ibu membeli soto babat di pasar
p ∨ q : Ibu memasak ayam goreng atau membeli soto babat di pasar.
b) p : Pak Bambang mengajar matematika
q : Pak Bambang mengajar bahasa inggris
p ∨ q : Pak Bambang mengajar matematika atau bahasa inggris
Soal No. 8
Diberikan nilai dari pernyataan p dan q sebagai berikut:
p
|
q
|
B
|
S
|
Tentukan nilai kebenaran dari disjungsi berikut:
a) p ∨ q
b) p ∨ ~q
c) ~p ∨ q
Pembahasan
Tabel lengkap dari disjungsi sebagai berikut:
.
|
p
|
q
|
p ∨ q
|
1
|
B
|
B
|
B
|
2
|
B
|
S
|
B
|
3
|
S
|
B
|
B
|
4
|
S
|
S
|
S
|
Dari data soal dapat diperoleh nilai dari negasi p maupun negasi q, tinggal dibalikkan saja B jadi S, S jadi B
p
|
q
|
~p
|
~q
|
B
|
S
|
S
|
B
|
a) p ∨ q
p bernilai B, q bernilai S
Pasangan B S menghasilkan nilai B (lihat tabel kebenaran nomor 2)
b) p ∨ ~q
p bernilai B, ~q bernilai B (kebalikan dari nilai q)
Pasangan B B menghasilkan nilai B (lihat tabel kebenaran nomor 1)
c) ~p ∨ q
~p bernilai S (kebalikan dari nilai p), q bernilai S
Pasangan S S menghasilkan nilai S (lihat tabel kebenaran nomor 4)
Soal No. 9
Negasi dari pernyataan " Matematika tidak mengasyikkan atau membosankan" adalah...
A. Matematika mengasyikkan atau membosankan
B. Matematika mengasyikkan atau tidak membosankan
C. Matematika mengasyikkan dan tidak membosankan
D. Matematika tidak mengasyikkan dan tidak membosankan
E. Matematika tidak mengasyikkan dan membosankan
Pembahasan
Untuk menentukan negasi dari suatu konjungsi atau disjungsi perhatikan dalil de Morgan berikut:
~(p ∧ q ) ≅ ~p ∨ ~q
~(p ∨ q) ≅ ~p ∧ ~ q
p : Matematika tidak mengasyikkan
q : Matematika membosankan
Negasi untuk p dan q masing-masing adalah:
~p : Matematika mengasyikkan
~q : Matematika tidak membosankan
Gunakan dalil de Morgan untuk negasi disjungsi
~(p ∨ q) ≅ ~p ∧ ~ q
sehingga
~p ∧ ~ q : Matematika mengasyikkan dan tidak membosankan
Soal No. 10
Tentukan negasi dari pernyataan:
a) Bogor hujan lebat dan Jakarta tidak banjir.
b) Hari ini tidak mendung dan Budi membawa payung
Pembahasan
Ingkaran (negasi) dari konjungsi.
a) Bogor hujan lebat dan Jakarta tidak banjir.
Ingat:
~(p ∧ q ) ≅ ~p ∨ ~q
Sehingga ingkarannya adalah:
Bogor tidak hujan lebat atau Jakarta banjir.
b) Hari ini tidak mendung dan Budi membawa payung
Ingat:
~(p ∧ q ) ≅ ~p ∨ ~q
Sehingga ingkarannya adalah:
Hari ini mendung atau Budi tidak membawa payung
Soal No. 11
Diberikan pernyataan:
p : Tahun ini kemarau panjang.
q : Tahun ini hasil padi meningkat.
Nyatakan dengan kata-kata:
a) p → q
b) ~p → ~q
c) p → ~q
Pembahasan
Implikasi, formatnya adalah "jika p maka q" sehingga:
a) p → q : Jika tahun ini kemarau panjang maka hasil padi meningkat
b) ~p → ~q : Jika tahun ini tidak kemarau panjang maka hasil padi tidak meningkat.
c) p → ~q : Jika tahun ini kemarau panjang maka hasil padi tidak meningkat.
Soal No. 12
Tentukan ingkaran dari pernyataan:
"Jika cuaca cerah maka maka Amir bermain sepakbola"
Pembahasan
Ingkaran dari sebuah implikasi p → q adalah p dan ~q
~(p → q) ≅ p ∧ ~ q
sehingga ingkaran dari pernyataan di atas adalah "Cuaca cerah dan Amir tidak bermain sepakbola"
Soal No. 13
Ingkaran dari pernyataan “Semua pasien mengharapkan sehat dan dapat beraktifitas kembali” adalah…
A. Beberapa pasien mengharapkan sehat dan dapat beraktifitas kembali.
B. Beberapa pasien mengharapkan tidak sehat atau tidak dapat beraktifitas kembali.
C. Beberapa pasien mengharapkan sehat tetapi tidak dapat beraktifitas kembali.
D. Beberapa pasien mengharapkan sehat tetapi dapat beraktifitas kembali.
E. Semua pasien mengharapkan sehat juga dapat beraktifitas kembali.
Pembahasan
Negasi dari sebuah pernyataan.
Bentuk yang sering muncul adalah:
“Semua pasien mengharapkan sehat dan dapat beraktifitas kembali”
Pernyataannya dalam bentuk (p ∧ q) jadi ingkarannya adalah ~p ∨ ~q.
Terjemahannya dalam kalimat menjadi
“Beberapa pasien mengharap tidak sehat atau tidak dapat beraktifitas kembali”. Cari kalimat yang sama di pilihannya.
Soal No. 14
Perhatikan pernyataan berikut:
"Jika cuaca mendung maka Charli membawa payung"
Tentukan konvers, invers dan kontraposisi dari pernyataan di atas!
Pembahasan
Dari implikasi p → q
p : Cuaca mendung
q : Charli membawa payung
Konversnya adalah q → p
yaitu "Jika Charli membawa payung maka cuaca mendung"
Inversnya adalah ~p → ~q
yaitu "Jika cuaca tidak mendung maka Charli tidak membawa payung"
Kontraposisinya adalah ~q → ~p
yaitu "Jika Charli tidak membawa payung maka cuaca tidak mendung"
Soal No. 15
Kontraposisi dari "Jika semua warga negara membayar pajak maka pembangunan berjalan lancar" adalah....
A. jika pembangunan tidak berjalan lancar maka ada warga negara yang tidak membayar pajak
B. jika tidak semua warga negara membayar pajak maka pembangunan tidak berjalan lancar
C. jika semua warga negara membayar pajak maka pembangunan tidak berjalan lancar
D. jika pembangunan berjalan lancar maka tidak semua warga negara membayar pajak
E. jika pembangunan tidak berjalan lancar maka semua warga negara tidak membayar pajak
(Soal Ebtanas 1995)
Pembahasan
p : semua warga negara membayar pajak
q : pembangunan berjalan lancar
Konversnya adalah ~q → ~p yaitu "Jika pembangunan tidak berjalan lancar maka ada warga negara yang tidak membayar pajak"
Soal No. 16
Premis 1 : Jika Budi rajin berolahraga maka badannya sehat.
Premis 2 : Budi rajin berolahraga.
Pembahasan
Modus Ponens
p → q
p
____
∴ q
Jika Budi rajin berolahraga maka badannya sehat.
p q
Budi rajin berolahraga
p
Kesimpulan adalah q : Badan Budi sehat
Soal No. 17
Tentukan kesimpulan dari :
Premis 1 : Jika hari cerah maka Budi bermain bola.
Premis 2 : Budi tidak bermain bola.
Pembahasan
p : Hari cerah
q : Budi bermain bola
Penarikan kesimpulan dengan prinsip Modus Tollens
p → q
~q
___
∴ ~p
Sehingga kesimpulannya adalah " Hari tidak cerah "
Soal No. 18
Tentukan kesimpulan dari :
Premis 1 : Jika Budi rajin belajar maka ia disayang ayah.
Premis 2 : Jika Budi disayang ayah maka ia disayang ibu.
Pembahasan
Penarikan kesimpulan dengan prinsip silogisme
p → q
q → r
___
∴ p → r
Sehingga kesimpulannya adalah " Jika Budi rajin belajar maka ia disayang ibu"
Soal No. 19
Diketahui pernyataan :
1. Jika hari panas, maka Ani memakai topi.
2. Ani tidak memakai topi atau ia memakai payung.
3. Ani tidak memakai payung.
Kesimpulan yang sah adalah...
A. Hari panas.
B. Hari tidak panas.
C. Ani memakai topi.
D. Hari panas dan Ani memakai topi.
E. Hari tidak panas dan Ani memakai topi.
Pembahasan
Premis (1) Jika hari panas, maka Ani memakai topi.
Premis (2) Ani tidak memakai topi atau ia memakai payung.
Premis (3) Ani tidak memakai payung.
p : Hari panas
q : Ani memakai topi
r : Ani memakai payung
Selesaikan terlebih dahulu premis (1) dan (2) kemudian digabungkan dengan premis (3)
Dari premis (1) dan (2)
Premis (1) Jika hari panas, maka Ani memakai topi.
Premis (2) Ani tidak memakai topi atau ia memakai payung.
p → q
~q ∨ r
Ingat bentuk berikut:
~q ∨ r ekivalen dengan q → r
sehingga bentuk di atas menjadi :
p → q
q → r
___
∴ p → r (Silogisme)
Dari sini gabungkan dengan premis ketiga:
p→ r
~r
___
∴ ~p (Modus Tollens)
Kesimpulan akhirnya adalah ~p yaitu "Hari tidak panas"
Soal No. 20
Diketahui premis-premis berikut:
Premis 1 : Jika masyarakat membuang sampah pada tempatnya maka lingkungan bersih.
Premis 2: Jika lingkungan bersih maka hidup akan nyaman.
Kesimpulan yang sah dari kedua premis tersebut adalah…
A. Jika masyarakat membuang sampah pada tempatnya maka hidup akan nyaman.
B. Masyarakat membuang sampah pada tempatnya maka hidup akan nyaman.
C. Jika masyarakat membuang sampah tidak pada tempatnya maka lingkungan tidak akan bersih.
D. Jika masyarakat membuang sampah pada tempatnya maka lingkungan tidak bersih.
E. Masyarakat membuang sampah pada tempatnya tetapi lingkungan tidak bersih.
Pembahasan
Penarikan kesimpulan. Premisnya berpola silogisme:
Sehingga kesimpulannya adalah “Jika masyarakat membuang sampah pada tempatnya maka hidup akan nyaman.”
Tidak ada komentar:
Posting Komentar