pengalaman belajar matematika: TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI DENGAN MATRIKS

Nasywa Kayla Zahra

XI IPS 2

Assalamualaikum Wr.Wb

Contoh 1 – Soal Translasi

Hasil translasi titik P1(3, –2) oleh T1 dilanjutkan dengan T2,

$T_{2} = \begin{pmatrix} 2 \\ 1 \end{pmatrix}$

menghasilkan titik P2 (8, 7). Komponen translasi dari T1 yang sesuai adalah ….

$\textrm{A.} \; \; \; \begin{pmatrix} 8 \\ 3 \end{pmatrix}$

$\textrm{B.} \; \; \; \begin{pmatrix} 3 \\ 8 \end{pmatrix}$

$\textrm{C.} \; \; \; \begin{pmatrix} 3 \\ 5 \end{pmatrix}$

$\textrm{D.} \; \; \; \begin{pmatrix} 1 \\ 8 \end{pmatrix}$

$\textrm{E.} \; \; \; \begin{pmatrix} 1 \\ 5 \end{pmatrix}$

Pembahasan:

Misalkan:

$T_{1} = \begin{pmatrix} a \\ b \end{pmatrix}$

Maka,

$T_{2} \bullet T_{1} = \begin{pmatrix} a + 4 \\ b + 1 \end{pmatrix}$

Perhatikan proses translasi berikut.

Mencari nilai a:

3 + a + 2 = 8
a + 5 = 8
a = 8 – 5 = 3

Mencari nilai b:

-2 + b + 1 = 7
b – 1 = 7
b = 7 + 1 = 8

Jadi, nilai translasi dari T1 adalah

$T_{1} = \begin{pmatrix} 3 \\ 8 \end{pmatrix}$

Jawaban: B

Contoh 2 – Soal dan Pembahasan Transformasi Geometri Refleksi

Persamaan garis 3x – y – 11 = 0 karena refleksi terhadap garis y = x, dilanjutkan oleh transformasi yang bersesuaian dengan matriks A,

$\begin{pmatrix} -3 & 2 \\ -1 & 1 \end{pmatrix}$

adalah ….
A. –2x – 7y –11 = 0
B. 2x + 7y – 11 = 0
C. –2x – 7y + 11 = 0
D. 2y – 7x + 11 = 0
E. 2x – 7y + 11 = 0

Pembahasan:

Pertama, cari hasil bayangan dari pencerminan terhadap garis y = x.

Matriks pencerminan terhadap garis y = x adalah:

Berdasarkan rumus di atas, dapat diperoleh kesimpulan bahwa x’ = y dan y’ = x. Substitusikan nilai tersebut pada persamaan 3x – y – 11 = 0 sehingga diperoleh persamaan berikut.

3x – y – 11 = 0
3y’ – x’ – 11 = 0
– x’ + 3y’ – 11 = 0

Kedua, langkah selanjutnya adalah transformasi yang bersesuaian dengan matriks A,

$\begin{pmatrix} -3 & 2 \\ -1 & 1 \end{pmatrix}$

Perhatikan langkah – langkahnya seperti berikut,

$\begin{pmatrix} x'' \\ y'' \end{pmatrix} = \begin{pmatrix} -3 & 2 \\ -1 & 1 \end{pmatrix} \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -3x' + 2y' \\ -x' + y' \end{pmatrix}$

Sehingga, diperoleh dua persamaan berikut.

–3x’ + 2y’ = x’’
– x’ + y’ = y’’

Berikutnya, akan dicari persamaan yang senilai dengan x’ dan y’:

Mencari nilai x’:

Metode eliminasi variabel

Mencari nilai y’:

Metode eliminasi variabel

Subtitusi hasil x’ dan y’ di atas pada persamaan – x’ + 3y’– 11 = 0:

$-x' + 3y' - 11 = 0$

$-\left( 2y'' - x'' \right) + 3\left( 3y'' - x'' \right) - 11 = 0$

$-2y'' + x'' + 9y'' - 3x'' - 11 = 0$

$2x'' - 7y'' + 11 = 0$

Jadi, hasil akhir transformasi dari persamaan 3x – y – 11 = 0 adalah 2x – 7y + 11 = 0.

Jawaban: E

Contoh 3 – Soal dan Pembahasan Transformasi Geometri Rotasi

Hasil pencerminan garis x – 2y – 2 = 0 terhadap sumbu y dan kemudian diputar dengan R[ O(0,0), 90o ] adalah ….
A. 2x – y – 4 = 0
B. x – 2y – 4 = 0
C. x – 2y – 2 = 0
D. 2x – y + 2 = 0
E. 2x – y – 4 = 0 \]

Pembahasan:

Hasil transformasi pencerminan terhadap sumbu y adalah:

Contoh Soal dan Pembahasan Transformasi Geometri Refleksi

Sehingga diperoleh x’ = – x dan y’ = y, selanjutnya substitusikan kedua nilai yang diperoleh pada persamaan x – 2y – 2 = 0.

x – 2y – 2 = 0
– x’ – 2y’ – 2 = 0

Transformasi selanjutnya adalah rotasi sebesar 90o yang berpusat di O(0, 0):

$\begin{pmatrix} x'' \\ y'' \end{pmatrix} = \begin{pmatrix} cos \; 90^{o} & -sin \; 90^{o} \\ sin \; 90^{o} & cos \; 90^{o} \end{pmatrix} \begin{pmatrix} x' \\ y' \end{pmatrix}$

$\begin{pmatrix} x'' \\ y'' \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x' \\ y' \end{pmatrix}$

$\begin{pmatrix} x'' \\ y'' \end{pmatrix} = \begin{pmatrix} -y' \\ x' \end{pmatrix}$

Substitusi nilai x’ = y’’ dan y’ = – x’’ pada persamaan –x’ – 2y’ – 2 = 0, akan diperoleh

– x’ – 2y’ – 2 = 0
– y’’ – 2(–x’’) – 2 = 0
– y’’ + 2x’’ – 2 = 0
2x’’ – y’’ + 2 = 0

Jadi, hasil pencerminan garis x – 2y – 2 = 0 terhadap sumbu y dan kemudian diputar dengan R[ O(0,0), 90o ] adalah 2x – y + 2 = 0.

Jawaban: D

Contoh 4 – Soal dan Pembahasan Transformasi Geometri Dilatasi

Dilatasi yang berpusat di titik (3, 1) dengan faktor skala 3, memetakan titik (5, b) ke titik (a, 10). Maka nilai a – b adalah ….
A. 15
B. 11
C. 5
D. 4
E. 2

Pembahasan:

Dilatasi dengan pusat (3, 1) dengan faktor skala 3 akan menghasilkan matriks transformasi berikut.

$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 5 - 3 \\ b- 1 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 2 \\ b- 1 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 6 \\ 3b - 3 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 9 \\ 3b - 2 \end{pmatrix}$

Sehingga dapat diperoleh nilai a dan b:

a = 9
3b – 2 = 10
3b = 12
b = 12 : 3 = 4

Jadi, nilai a – b = 9 – 4 = 5

Jawaban: C

contoh soal 5

Persamaan peta garis 3x – 4y = 12, karena refleksi terhadap garis y – x = 0, dilanjutkan oleh transformasi yang bersesuaian dengan matriks $\left(\begin{array}{rr} -3&5\\ -1&1\end{array}\right)$ adalah… (UAN ’03)

Pembahasan 1:

Diketahui matriksnya:

Rotasi = $\left(\begin{array}{rr} 0&1\\ 1&0\end{array}\right)$

Transformasi = $\left(\begin{array}{rr} -3&5\\ -1&1\end{array}\right)$

Persamaan garis direfleksi kemudian ditransformasi adalah:

$\left(\begin{array}{r} x'\\ y'\end{array}\right) = \left(\begin{array}{rr} -3&5\\ -1&1\end{array}\right) \left(\begin{array}{rr} 0&1\\ 1&0\end{array}\right) \left(\begin{array}{r} x\\ y\end{array}\right) = \left(\begin{array}{rr} 5&-3\\ 1&-1\end{array}\right) \left(\begin{array}{r} x'\\ y'\end{array}\right)$

$\left(\begin{array}{r} x\\ y\end{array}\right) = - \frac{1}{2} \left(\begin{array}{rr} -1&3 \\ -1&5\end{array} \right) \left(\begin{array}{r} x'\\ y'\end{array}\right) = \begin{pmatrix} \frac{x'-3y'}{2} \\ \frac{x'-5y'}{2} \end{pmatrix}$

Kemudian disubstitusikan:

$3x - 4y = 12 \overset{substitusi}{\rightarrow}3 (\frac{x'- 3y'}{2}) - 4(\frac{x'-5y'}{2}) = 12$

$3(x' - 3y') - 4(x'- 5y') = 24$

$3x' - 9y' - 4x' + 20y' =24$

$-x' + 11y' =24$

Hasilnya:

$11y - x =24$

Contoh Soal 6

Pencerminan terhadap sumbu x adalah A, pencerminan terhadap sumbu y adalah B dan rotasi 180o terhadap puasat O adalah H. Tentukan matriks B(A(HA)). (UMPTN ’90)

Pembahasan 2:

Diketahui:

Pencerminan terhadap sumbu $x,A = \left(\begin{array}{rr} 1&0\\ 0&-1\end{array}\right)$
Pencerminan terhadap sumbu $y,B = \left(\begin{array}{rr} -1&0\\ 0&1\end{array}\right)$
Rotasi 180o, $H = \left(\begin{array}{rr} cos 180 &-sin180 \\ sin 180 & cos 180\end{array}\right) = \left(\begin{array}{rr} -1&0\\ 0&-1\end{array}\right)$

Maka:

$B(A(HA)) = \left(\begin{array}{rr} -1&0\\ 0&1\end{array}\right) ( \left(\begin{array}{rr} 1&0\\ 0&-1\end{array}\right) [ \left(\begin{array}{rr} -1&0\\ 0&-1\end{array}\right) \left(\begin{array}{rr} -1&0\\ 0&-1\end{array}\right) ]))$

$= \left(\begin{array}{rr} -1&0\\ 0&1\end{array}\right) ( \left(\begin{array}{rr} 1&0\\ 0&-1\end{array}\right) \left(\begin{array}{rr} -1&0\\ 0&1\end{array}\right) )$

$= \left(\begin{array}{rr} -1&0 \\ 0&1\end{array}\right) \left(\begin{array}{rr} -1&0\\ 0&-1\end{array}\right)$

$= \left(\begin{array}{rr} 1&0\\ 0&-1\end{array}\right)$

contoh soal 7

Oleh matriks $A = \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right)$ , titik $P(1, 2)$ dan titik Q masing-masing ditransformasikan ke titik $P'(2, 3)$ dan $Q'(2,0)$ . Tentukan koordinat titik Q. (SPMB’04)

Pembahasan 3:

Mencari nilai a dari transformasi P:

$\left(\begin{array}{r} x'\\ y'\end{array}\right)= \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right) \left(\begin{array}{r} x\\ y\end{array}\right)\overset{sehingga}{\rightarrow}\left(\begin{array}{r} 2\\ 3\end{array}\right) = \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right) \left(\begin{array}{r} 1\\ 2\end{array}\right)\overset{menjadi}{\rightarrow}\left(\begin{array}{r} 2\\ 3\end{array}\right) = \left(\begin{array}{rr} 2 + 3a\\ 3 + 2a\end{array}\right)$

$a = 0$

Sehingga matriksnya:

$A = \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right) = \left(\begin{array}{rr} 2&0\\ 1&1\end{array}\right)$

Mencari titik Q:

$\left(\begin{array}{r} x'\\ y'\end{array}\right) = \left(\begin{array}{rr} 2&0\\ 1&1\end{array}\right) \left(\begin{array}{r} x\\ y\end{array}\right) \overset{sehingga}{\rightarrow} \left(\begin{array}{r} x\\ y\end{array}\right) = \frac{1}{2} \left(\begin{array}{rr} 1&0\\ -1&2\end{array}\right) \left(\begin{array}{r} x'\\ y'\end{array}\right) \overset{disubstitusi} = {\rightarrow} \left(\begin{array}{r} x\\ y\end{array}\right) = \frac{1}{2} \left(\begin{array}{rr} 1&0\\ -1&2\end{array}\right) \left(\begin{array}{r} 2\\0\end{array}\right)$

$\left(\begin{array}{r} x\\ y\end{array}\right) = \left(\begin{array}{r} 1\\ -1\end{array}\right)$

Sehingga:

$Q(1, -1)$

1. Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah. . .

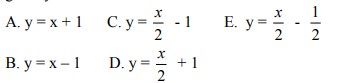
soal transformasi geometri no 1

Jawaban : C

Pembahasan :

soal transformasi geometri dan jawaban no 1

2. Persamaan bayangan kurva y = x² – 2x – 3 oleh rotasi [0, 180°], kemudian dilanjutkan oleh pencerminan terhadap garis y = -x adalah ….

A. y = x² – 2x – 3

B. y = x² – 2x + 3

C. y = x² + 2x + 3

D. x = y² – 2y – 3

E. x = y² + 2y + 3

Jawaban : D

Pembahasan :

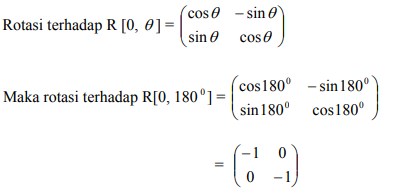
soal transformasi geometri dan jawaban no 2

Rotasi sudut-sudut yang lain dapat dihitung sendiri menggunakan kaidah trigonometri.

pencerminan terhadap garis y = -x

soal transformasi geometri dan jawaban no 2-1

3. Persamaan bayangan dari lingkaran x² +y² +4x – 6y – 3 = 0 oleh transformasi yang berkaitan dengan matriks 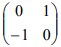adalah….

A. x² + y² – 6x – 4y- 3 = 0

B. X² + y² – 6x + 4y- 3 = 0

C. x² + y² + 6x – 4y- 3 = 0

D. x² + y² – 4x + 6y- 3 = 0

E. x² + y² + 4x – 6y+ 3 = 0

Jawaban : A

Pembahasan :

soal transformasi geometri dan jawaban no 3

4. T1 dan T2 adalah transformasi yang masing-masing bersesuaian dengan 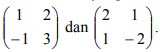soal transformasi geometri no 4 Ditentukan T = T1 o T2 , maka transformasi T bersesuaian dengan matriks…

Jawaban : E

Pembahasan :

soal transformasi geometri dan jawaban no 4

5. Ditentukan matriks transformasi .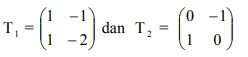 soal transformasi geometri no 5 Hasil transformasi titik (2,-1) terhadap T1 dilanjutkan T2 adalah….

A. (-4,3)

B. (-3,4)

C. (3,4)

D. (4,3)

E. (3,-4)

Jawaban : A

Pembahasan :

soal transformasi geometri dan jawaban no 5

6. Persamaan bayangan garis y = -6x + 3 karena transformasi oleh matriks soal transformasi geometri no 6 kemudian dilanjutkan dengan matriks 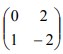adalah…

A. x + 2y + 3 = 0

B. x + 2y – 3 = 0

C. 8x – 19y + 3 = 0

D. 13x + 11y + 9 = 0

E. 13x + 11y – 9 = 0

Jawaban : E

Pembahasan :

soal transformasi geometri dan jawaban no 6

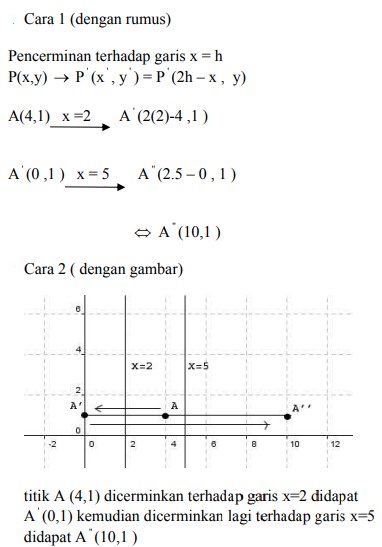
7. Bayangan titik A (4,1) oleh pencerminan terhadap garis x =2 dilanjutkan pencerminan terhadap garis x = 5 adalah titik….

A. A” (8,5)

B. A” (10,1)

C. A” (8,1)

D. A” (4,5)

E. A” (20,2)

Jawaban : B

Pembahasan :

soal transformasi geometri dan jawaban no 7

8. T1 adalah transformasi yang bersesuaian dengan matriks 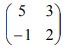soal transformasi geometri no 8 dan T2 adalah transformasi yang bersesuaian dengan matriks 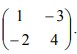Bayangan A (m,n) oleh transformasi T1 o T2 adalah (-9,7). Nilai m+n sama dengan…

A. 4

B. 5

C. 6

D. 7

E. 8

Jawaban : B

Pembahasan :

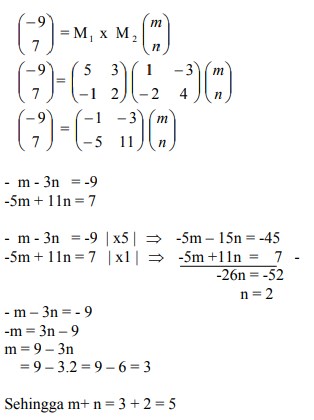
soal transformasi geometri dan jawaban no 8

9. Bayangan ∆ABC dengan A(2,1), B(6,1), C(5,3) karena refleksi terhadap sumbu y dilanjutkan rotasi (0,90°) adalah…

A. A” (-1,-2), B” (1,6) dan C” (-3,-5)

B. A” (-1,-2), B” (1,-6) dan C” (-3,-5)

C. A” (1,-2), B” (-1,6) dan C” (-3,5)

D. A” (-1,-2), B” (-1,-6) dan C” (-3,-5)

E. A” (-1,2), B” (-1,-6) dan C” (-3,-5)

Jawaban : D

Pembahasan :

soal transformasi geometri dan jawaban no 9

10. Persamaan peta kurva y = x² – 3x + 2 karena pencerminan terhadap sumbu x dilanjutkan dilatasai dengan pusat O dan factor skala 3 adalah…

A. 3y + x² – 9x + 18 = 0

B. 3y – x² + 9x – 18 = 0

C. 3y – x² + 9x + 18 = 0

D. 3y + x² + 9x + 18 = 0

E. y + x² + 9x – 18 = 0

Jawaban : A

Pembahasan :

pencerminan terhadap sumbu x:

P ( x , y ) → P ‘ ( x , – y )

Dilatasi terhadap titik pusat O(0,0) dengan factor skala 3 :

[O, k] : P(x,y) → P'(kx, ky)

[O,3k] : P(x,y) → P'(3x, 3y)

pencerminan terhadap sumbu x dilanjutkan dilatasai
dengan pusat O dan factor skala 3 :

P(x,y) → P ‘(x, -y) → P ”(3x, -3y)

soal transformasi geometri dan jawaban no 10

11. Luas bayangan persegipanjang PQRS dengan

P(-1,2), Q(3,2), R (3,-1), S(-1,-1)

karena dilatasi [0,3] dilanjutkan rotasi pusat O bersudut π/2 adalah…

A. 36

B. 48

C.72

D. 96

E. 108

Jawaban : E

Pembahasan :

dilatasi [0,3] :

[O,3k] : P(x,y) → P ‘(3x, 3y)

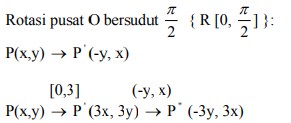
soal transformasi geometri dan jawaban no 11

Sehingga :

P(x,y) → P” (-3y, 3x)

P(-1,2), Q(3,2), R (3,-1), S(-1,-1)

P(-1,2) → P” (-6,-3)

Q(3,2) → Q” (-6,9)

R (3,-1) → R” (3,9)

S(-1,-1) → S” (3,-3)

Buat sketsa gambarnya:

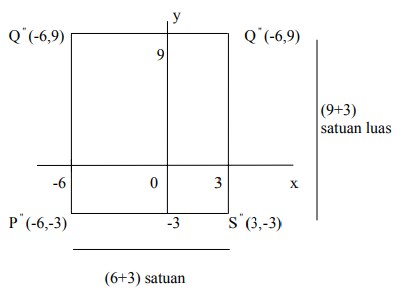
soal transformasi geometri dan jawaban no 11-1

Sehingga luas transformasinya adalah :

Panjang (p) x lebar (l) = 12 x 9 = 108 satuan luas

12. Segitiga ABC dengan A(2,1), B(6,1), C(6,4) ditransformasikan dengan matriks transformasi 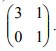soal transformasi geometri no 12 Luas bangun hasil transformasi segitiga ABC adalah….

A. 56 satuan luas

B. 36 satuan luas

C. 28 satuan luas

D. 24 satuan luas

E. 18 satuan luas

Jawaban : E

Pembahasan :

misalkan T = 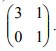soal transformasi geometri no 12 maka

Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC |det T| = |ad –bc| = |3-0| = 3

luas ∆ ABC :

buat sketsa gambar :

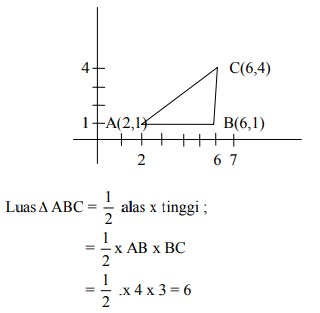
soal transformasi geometri dan jawaban no 12

Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC

= 3 x 6 = 18 satuan luas

13. Tentukan bayangan lingkaran (x-3)2 + (y+1)2 = 4 jika ditranslasikan

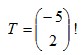
a. 5

b. 4

c. 3

d. 2

e. 1

Jawaban : B

Pembahasan :

Ambil sembarang titik P(a,b) pada lingkaran (x-3)2 + (y+1)2 = 4 sehingga diperoleh (a-3)2 + (b+1)2 = 4

soal transformasi geometri no 13-1

14. ABCD adalah sebuah persegi dengan koordinat titik-titik sudut A(1,1), B(2,1), C(2,2) dan D(1,2). Tentukan peta atau bayangan dari titik-titik sudut persegi itu oleh dilatasi [O,2]!

Jawaban :

Pembahasan :

soal transformasi geometri no 14

15. Jika titik A(15,8) dicerminkan terhadap garis x=7, maka bayangan titik A adalah titik A’ dengan koordinat….

Jawaban :

Pembahasan :

soal transformasi geometri no 15

Baca Juga : 15+ Soal Sistem Persamaan Linear Dua Variabel (SPLDV) [+Pembahasan]

16. Titik A(a,b) dicerminkan terhadap garis x=2 menghasilkan bayangan titik A’(0,2), maka nilai (a,b) berturut-turut adalah….

a. 2 , 4

b. 4 , 2

c. 2 , 2

d. 3 , 1

e. 1 , 3

Jawaban : B

Pembahasan :

soal transformasi geometri no 16

17. Titik A’(-16,24) merupakan bayangan dari titik A(x,y) yang didilatasikan dengan pusat O(0,0) dan faktor skala -4. Koordinat titik A adalah….

Jawaban :

Pembahasan :

soal transformasi geometri no 17

18. Tentukan persamaan peta dari garis 3x – 5y + 15 = 0 oleh pencerminan terhadap sumbu x!

Jawaban :

Pembahasan :

soal transformasi geometri no 18

19. Tentukan persamaan peta dari garis 3x-5y+15=0 oleh dilatasi terhadap pusat O(0,0) dengan faktor skala 5!

Jawaban :

Pembahasan :

soal transformasi geometri no 19

20. Lingkaran x² + y² – 6x + 2y + 1 = 0. Jika ditransformasikan dengan dilatasi [O,4], persamaan bayangannya adalah….

Jawaban :

Pembahasan :

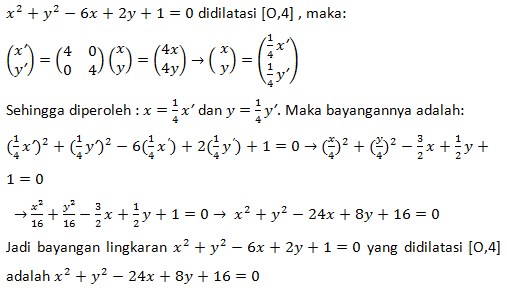
soal transformasi geometri no 20

Contoh 1
Peta titik A(2, 3) oleh pencerminan terhadap garis y = x adalah ...

Jawab :
$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}] [\begin{matrix} 2 \\ 3 \end{matrix}]$

$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} 3 \\ 2 \end{matrix}]$

Jadi, peta titik A adalah A'(3, 2)

Contoh 2
Bayangan titik P jika dicerminkan terhadap sumbu x adalah (4, -2 ). Koordinat titik P adalah ...

Jawab :
$[\begin{matrix} - 4 \\ - 2 \end{matrix}] = [\begin{matrix} 1 & - 0 \\ 0 & - 1 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$

$[\begin{matrix} - 4 \\ - 2 \end{matrix}] = [\begin{matrix} - x \\ - y \end{matrix}]$

Dari persamaan matriks diatas kita peroleh
4 = x → x = 4
-2 = -y → y = 2

Jadi, koordinat titik P adalah (4, 2)

Contoh 3
Bayangan garis 2x + y - 3 = 0 jika dicerminkan terhadap pusat O adalah ...

Jawab :
$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} - 1 & 0 \\ 0 & - 1 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$

$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} - x \\ - y \end{matrix}]$

Dari persamaan matriks diatas kita peroleh
x' = -x → x = -x'
y' = -y → y = -y'

Substitusi x = -x' dan y = -y' ke garis 2x + y - 3 = 0
2(-x') + (-y') - 3 = 0
-2x' - y' - 3 = 0
2x' + y' + 3 = 0

Jadi, bayangannya adalah 2x + y + 3 = 0

Matriks Rotasi (Perputaran)

Misalkan peta titik A(x, y) oleh rotasi dengan pusat O sejauh θ adalah A'(x', y'). Perhatikan gambar berikut

Dari segitiga siku-siku OBA diperoleh
x = r cos α
y = r sin α

Dari segitiga siku-siku OCA' diperoleh
x' = r cos (α + θ )
x' = r (cos α cos θ - sin α sin θ)
x' = r cos α cos θ - r sin α sin θ
x' = x cos θ - y sin θ

y' = r sin (α + θ )
y' = r (sin α cos θ + cos α sin θ)
y' = r sin α cos θ + r cos α sin θ
y' = y cos θ + x sin θ
y' = x sin θ + y cos θ

Diperoleh
x' = x cos θ - y sin θ
y' = x sin θ + y cos θ

Dalam persamaan matriks kita tulis $[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} c o s θ & - s i n θ \\ s i n θ & c o s θ \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$
Jadi, matriks yang bersesuaian dengan rotasi terhadap pusat O sebesar θ adalah $M_{[O, θ]} = [\begin{matrix} c o s θ & - s i n θ \\ s i n θ & c o s θ \end{matrix}]$

Contoh 4
Titik A(-4, 3) dipetakan oleh rotasi dengan pusat O sejauh 90° searah jarum jam. Peta titik A adalah ...

Jawab :
Searah jarum jam berarti θ = -90°

Ingat :
sin (-θ) = - sin θ
cos (-θ) = cos θ

$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} c o s (- 90^{\circ}) & - s i n (- 90^{\circ}) \\ s i n (- 90^{\circ}) & c o s (- 90^{\circ}) \end{matrix}] [\begin{matrix} - 4 \\ 3 \end{matrix}]$

$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} 0 & 1 \\ - 1 & 0 \end{matrix}] [\begin{matrix} - 4 \\ 3 \end{matrix}]$

$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} 3 \\ 4 \end{matrix}]$

Jadi, peta titik A adalah A'(3, 4)

Contoh 5
Bayangan garis y = 2x + 1 oleh rotasi dengan pusat O sebesar 180° adalah ...

Jawab :
$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} c o s 180^{\circ} & - s i n 180^{\circ} \\ s i n 180^{\circ} & c o s 180^{\circ} \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$

$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} - 1 & 0 \\ 0 & - 1 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$

$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} - x \\ - y \end{matrix}]$

Dari persamaan matriks diatas diperoleh
x' = -x → x = -x'
y' = -y → y = -y'

Substitusi x = -x' dan y = -y' ke garis y = 2x + 1
-y' = 2(-x') + 1
-y' = -2x' + 1
y' = 2x' - 1

Jadi, bayangannya adalah y = 2x - 1

Misalkan peta titik A(x, y) oleh rotasi dengan pusat P(a, b) sejauh θ adalah A'(x', y'). Perhatikan gambar berikut :

Dari segitiga siku-siku PBA diperoleh
x - a = r cos α
y - b = r sin α

Dari segitiga siku-siku PCA' diperoleh
x' - a = r cos (α + θ)
x' - a = r (cos α cos θ - sin α sin θ)
x' - a = r cos α cos θ - r sin α sin θ
x' - a = (x - a) cos θ - (y - b) sin θ

y' - b = r sin (α + θ)
y' - b = r (sin α cos θ + cos α sin θ)
y' - b = r sin α cos θ + r cos α sin θ
y' - b = (y - b) cos θ + (x - a) sin θ
y' - b = (x - a) sin θ + (y - b) cos θ

Diperoleh
x' - a = (x - a) cos θ - (y - b) sin θ
y' - b = (x - a) sin θ + (y - b) cos θ

Dalam persamaan matriks kita tulis $[\begin{matrix} x^{'} - a \\ y^{'} - b \end{matrix}] = [\begin{matrix} c o s θ & - s i n θ \\ s i n θ & c o s θ \end{matrix}] [\begin{matrix} x - a \\ y - b \end{matrix}]$

Contoh 6
Persamaan bayangan parabola y = x² + 2x + 1 jika dirotasi dengan pusat P(2, -3) sejauh 270° adalah ...

Jawab :
$[\begin{matrix} x^{'} - 2 \\ y^{'} + 3 \end{matrix}] = [\begin{matrix} c o s 270^{\circ} & - s i n 270^{\circ} \\ s i n 270^{\circ} & c o s 270^{\circ} \end{matrix}] [\begin{matrix} x - 2 \\ y + 3 \end{matrix}]$

$[\begin{matrix} x^{'} - 2 \\ y^{'} + 3 \end{matrix}] = [\begin{matrix} 0 & 1 \\ - 1 & 0 \end{matrix}] [\begin{matrix} x - 2 \\ y + 3 \end{matrix}]$

$[\begin{matrix} x^{'} - 2 \\ y^{'} + 3 \end{matrix}] = [\begin{matrix} y + 3 \\ - x + 2 \end{matrix}]$

Dari persamaan matriks diatas kita peroleh
x' - 2 = y + 3 → y = x' - 5
y' + 3 = -x + 2 → x = -y' - 1

Substitusi x dan y ke parabola y = x² + 2x + 1
x' - 5 = (-y' - 1)² + 2(-y' - 1) + 1
x' - 5 = (y')² + 2y' + 1 - 2y' - 2 + 1
x' - 5 = (y')²
(y')² = x' - 5

Jadi, persamaan bayangannya adalah y² = x - 5

Matriks Dilatasi (Perkalian)

Misalkan peta titik A(x, y) oleh dilatasi dengan pusat O dan faktor skala k adalah A'(x', y'). Perhatikan gambar berikut :

Sebagai catatan, titik A'(x', y') dapat berada disepanjang garis m, tergantung nilai k.

Berdasarkan gambar diatas, koordinat A'(x', y') dapat kita tulis dalam persamaan
x' = kx ⇔ x' = kx + 0y
y' = ky ⇔ y' = 0x + ky

Dalam persamaan matrik kita tulis $[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} k & 0 \\ 0 & k \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$ dengan matriks dilatasinya $M_{[O, k]} = [\begin{matrix} k & 0 \\ 0 & k \end{matrix}]$ Untuk pusat (a, b), persamaan matriksnya adalah $[\begin{matrix} x^{'} - a \\ y^{'} - b \end{matrix}] = [\begin{matrix} k & 0 \\ 0 & k \end{matrix}] [\begin{matrix} x - a \\ y - b \end{matrix}]$

Contoh 7
Persamaan bayangan lingkaran x² + y² = 5 oleh dilatasi dengan pusat O dan faktor skala 2 adalah ...

Jawab :
$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} 2 & 0 \\ 0 & 2 \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$
https://soalkimia.com/contoh-soal-transformasi-geometri/
$[\begin{matrix} x^{'} \\ y^{'} \end{matrix}] = [\begin{matrix} 2 x \\ 2 y \end{matrix}]$

Dari persamaan matriks diatas kita peroleh
x' = 2x → x = $\frac{1}{2}$ x'
y' = 2y → y = $\frac{1}{2}$ y

Substitusi x dan y ke persamaan x² + y² = 5
( $\frac{1}{2}$ x')² + ( $\frac{1}{2}$ y')² = 5
$\frac{1}{4}$ (x')² + $\frac{1}{4}$ (y')² = 5 (kali 4)
(x')² + (y')² = 20

Jadi, bayangannya adalah x² + y² = 20

Contoh 8
Peta titik R(1, 3) oleh dilatasi dengan pusat (-2, 4) dan faktor skala -2 adalah ...

Jawab :
Titik R : (x, y) = (1, 3)
Pusat dilatasi : (a, b) = (-2, 4)
Faktor skala : k = -2
Peta titik R : (x', y') = ?

Persamaan matriksnya
$[\begin{matrix} x^{'} - a \\ y^{'} - b \end{matrix}] = [\begin{matrix} k & 0 \\ 0 & k \end{matrix}] [\begin{matrix} x - a \\ y - b \end{matrix}]$

$[\begin{matrix} x^{'} + 2 \\ y^{'} - 4 \end{matrix}] = [\begin{matrix} - 2 & 0 \\ 0 & - 2 \end{matrix}] [\begin{matrix} 1 + 2 \\ 3 - 4 \end{matrix}]$

$[\begin{matrix} x^{'} + 2 \\ y^{'} - 4 \end{matrix}] = [\begin{matrix} - 2 & 0 \\ 0 & - 2 \end{matrix}] [\begin{matrix} 3 \\ - 1 \end{matrix}]$

$[\begin{matrix} x^{'} + 2 \\ y^{'} - 4 \end{matrix}] = [\begin{matrix} - 6 \\ 2 \end{matrix}]$

Dari persamaan matriks diatas kita peroleh
x' + 2 = -6 → x' = -8
y' - 4 = 2 → y' = 6

Jadi, peta titik R adalah R'(-8, 6)

https://smatika.blogspot.com/2017/11/matriks-transformasi-geometri.html

https://soalkimia.com/contoh-soal-transformasi-geometri/

https://idschool.net/sma/rumus-pada-transformasi-geometri-translasi-refleksi-rotasi-dan-dilatasi/

https://www.studiobelajar.com/transformasi-geometri/

pengalaman belajar matematika

Minggu, 27 September 2020

TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI DENGAN MATRIKS

Contoh 1 – Soal Translasi

Contoh 2 – Soal dan Pembahasan Transformasi Geometri Refleksi

Contoh 3 – Soal dan Pembahasan Transformasi Geometri Rotasi

Contoh 4 – Soal dan Pembahasan Transformasi Geometri Dilatasi

Contoh Soal 6

Baca Juga : 15+ Soal Sistem Persamaan Linear Dua Variabel (SPLDV) [+Pembahasan]

Matriks Rotasi (Perputaran)

Matriks Dilatasi (Perkalian)

Tidak ada komentar:

Posting Komentar