soal-soal matriks
Nasywa Kayla Zahra

XI IPS 2
26
Kesamaan matriks, soal determinan matriks berordo 3x3 dan 2x2, soal kofaktor matriks berordo 3x3 dan 2x2, serta invers matriks berordo 3x3 dan 2x2
PERSAMAAN MATRIKS
RUMUS
(1) Jika A x B = C maka B =A-1 x C
(2) Jika A x B = C maka A = C x A-1
CONTOH SOAL
01. Diketahui matriks

maka tentukanlah matriks B jika B x A = C
02. Tentukan himpunan penyelesaian sistem persamaan 2x – 3y = 8 dan x + 2y = –3 dengan metoda:
(a) Invers matriks (b) Determinan
Jawab



(a) Invers matriks (b) Determinan
Jawab
soal 3

p + 2 = -3 (posisinya sama)
p + 2 = -3
p + 2 = -3
- pindahkan +2 ke ruas kanan sehingga menjadi -2
p = -3 -2
p = -5
Lanjut!!
q - 2 = 5 (posisinya sama)
q -2 = 5
- pindahkan -2 ke ruas kanan sehingga menjadi +2
q = 5 + 2
q = 7.
Jadi nilai :
- p = -5
- q = 7
p - 2 = 7
05. Berapakah nilai dari p dan q pada persamaan matriks berikut :
- pindahkan -2 ke ruas kanan sehingga menjadi +2
p = 7 + 2
p = 9
Lanjut mencari nilai q.
q + 2 = 5
- pindahkan + 2 ke ruas kanan sehingga menjadi -2
q = 5 - 2
q = 3.
Jadi nilai :
- p = 9
- q = 3


2p + 2 = 10, dan
3q + 3 = -6
3q + 3 = -6
Nilai p dulu..
2p + 2 = 10

 2. Nilai determinan dari matriks A di atas adalah ....
2. Nilai determinan dari matriks A di atas adalah ....
⇔ det(B) = 4 - 6
⇔ det(B) = -2
Jika nilai determinan matriks B adalah 4, maka nilai x adalah ......?
⇔ 4 = 16 - 4X
⇔ 4x = 16 - 4
⇔ 4x = 12
⇔ x = 3
Agar determinan matriks A sama dengan dua kali determinan B, maka nilai x yang memenuhi adalah....
Jika determinan matriks A = -5, maka determinan matriks B adalah...?
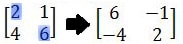











2p + 2 = 10
- pindahkan + 2 ke ruas kanan sehingga menjadi -2
2p = 10 - 2
2p = 8
- untuk mendapatkan p, bagi 8 dengan 2
p = 8 : 2
p = 4.
Sekarang nilai q
3q + 3 = -6
- pindahkan +3 ke ruas kanan menjadi -3
3q = -6 - 3
3q = -9
- untuk mendapatkan q, bagi -9 dengan 3
q = -9 : 3
q = -3.
Jadi nilai :
- p = 4
- q = -3
SOAL DETERMINAN MATRIKS BERORDO 3X3 DAN 2X2
Contoh soal
Determinan Matriks Ordo 2x2
Tentukanlah determinan matriks berikut!

Pembahasan:
 2. Nilai determinan dari matriks A di atas adalah ....
2. Nilai determinan dari matriks A di atas adalah ....A =
|
det(B) =
= (1)(4) - (2)(3)
|
⇔ det(B) = 4 - 6
⇔ det(B) = -2
3. . B =
|
Jika nilai determinan matriks B adalah 4, maka nilai x adalah ......?
det(A) =
= (2)(8) - (x)(4)
|
⇔ 4 = 16 - 4X
⇔ 4x = 16 - 4
⇔ 4x = 12
⇔ x = 3
4. Terdapat dua buah matriks, yaitu : matriks A dan B seperti dibawwah ini :
A =
B =
|
|
Agar determinan matriks A sama dengan dua kali determinan B, maka nilai x yang memenuhi adalah....
Determinan untuk matriks A adalah :
⇔ det(A) = 2x2 - 6
Determinan untuk matriks B adalah :
⇔ det(B) = 4x + 9
Dikatakan determinan matriks A sama dengan dua kali determinan B,sehingga :
⇔ det(A) = 2 det(B)
⇔ 2x2 - 6 = 2(4x + 9)
⇔ 2x2 - 6 = 8x + 18
⇔ 2x2 - 8x - 24 = 0
⇔ x2 - 4x - 12 = 0
⇔ (x - 6)(x + 2) = 0
⇔x = 6 atau x = -2
det(A) =
= (x)(2x) - (2)(3)
|
⇔ det(A) = 2x2 - 6
Determinan untuk matriks B adalah :
det(B) =
= (4)(x) - (3)(-3)
|
⇔ det(B) = 4x + 9
Dikatakan determinan matriks A sama dengan dua kali determinan B,sehingga :
⇔ det(A) = 2 det(B)
⇔ 2x2 - 6 = 2(4x + 9)
⇔ 2x2 - 6 = 8x + 18
⇔ 2x2 - 8x - 24 = 0
⇔ x2 - 4x - 12 = 0
⇔ (x - 6)(x + 2) = 0
⇔x = 6 atau x = -2
5. Diketahui matriks A dan B seperti dibawah ini :
A =
B =
|
|
Jika determinan matriks A = -5, maka determinan matriks B adalah...?
Determinan untuk matriks A adalah :
⇔ det(A) = ad - bc = -5
Determinan untuk matriks B adalah :
⇔ det(B) = 3ad - 3bc
⇔ det(B) = 3(ad - bc)
⇔ det(B) = 3.det(A)
⇔ det(B) = 3(-5)
⇔ det(B) = -15)
det(A) =
= (a)(d) - (b)(c)
|
⇔ det(A) = ad - bc = -5
Determinan untuk matriks B adalah :
det(B) =
= (3a)(d) - (3b)(c)
|
⇔ det(B) = 3ad - 3bc
⇔ det(B) = 3(ad - bc)
⇔ det(B) = 3.det(A)
⇔ det(B) = 3(-5)
⇔ det(B) = -15)
CONTOH SOAL DETERMINAN MATRIKS BERORSO 3X3
Contoh.1
Tentukan Nilai Determinan dari matriks ordo 3x3 berikut :
Jawab :
Nilai determinan untuk matriks di atas adalah sebagai berikut:
Contoh.2
Tentukan Nilai Determinan dari matriks ordo 3x3 berikut :
Jawab :
Nilai determinan untuk matriks di atas adalah sebagai berikut:

Tentukanlah A^-1
Jawab : invers A =

maka invers A =

hasilnya


Tentukan Nilai Determinan dari matriks ordo 3x3 berikut :
A =
|
Jawab :
Nilai determinan untuk matriks di atas adalah sebagai berikut:
det(A) =
|
|
det(A) = 2.4.1 + 3.3.7 + 4.5.0 – 4.4.7 – 2.3.0 – 3.5.1
= 8 + 63 + 0 – 112 – 0 – 15
= – 56Contoh.2
Tentukan Nilai Determinan dari matriks ordo 3x3 berikut :
B =
|
Jawab :
Nilai determinan untuk matriks di atas adalah sebagai berikut:
det(B) =
|
|
det(A) = (1.1.2) + (2.4.3) + (3.2.1) – (3.1.3) – (1.4.1) – (2.2.2)
= 2 + 24 + 6 – 9 – 4 – 8
= 11INVERS MATRIKS BERORDO 3X3 DAN 2X2
INVERS MATRIKS BERORDO 2X2
contoh soal
1. Diketahui matriks A =
Tentukanlah A^-1
Jawab : invers A =
maka invers A =
hasilnya
2. 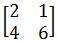
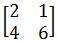
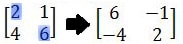
Contoh soal
Tentukanlah invers dari matriks berikut.

Pembahasan:

Invers Matriks Ordo 3x3
Contoh soal
Tentukan invers matriks berikut dengan menggunakan adjoin!

Penyelesaian:

Oke, berdasarkan rumus di atas, kita membutuhkan determinan dan adjoin matriks A. Pertama, kita cari terlebih dahulu determinan matriks A menggunakan metode yang sudah dijelaskan sebelumnya. Bisa dengan cara aturan Sarrus ataupun metode minor-kofaktor. Misalnya, kita akan menggunakan metode Sarrus, sehingga:

Kemudian, kita tentukan adjoin matriks dengan mencari kofaktor matriks A tersebut.

Oleh karena itu,

Jadi,

contoh soal 2.

Soal Kofaktor Matriks berordo 3 x 3 dan 2 x 2
diketahui matrik A sebagai berikut:


Jadi matrik kofaktor (C) dari matrik di atas adalah:







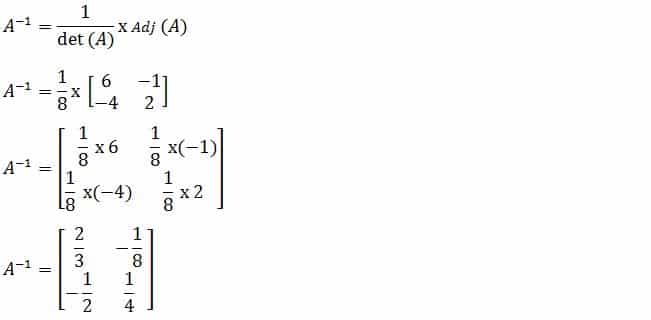

Tidak ada komentar:
Posting Komentar