PENGERTIAN TURUNAN DAN SIFAT-SIFATNYA BERSAMA CONTOH SOALNYA

Nasywa Kayla Zahra

XI IPS 2

27

Assalamualaikum Wr.Wb

Definisi Turunan

Turunan merupakan suatu perhitungan terhadap perubahan nilai fungsi karena perubahan nilai input (variabel).

Turunan dapat disebut juga sebagai diferensial dan proses dalam menentukan turunan suatu fungsi disebut sebagai diferensiasi.

https://rumuspintar.com/turunan/

Sifat-sifat Turunan

1. Jika $f(x)=c$ dimana $c$ adalah konstanta, maka turunannya adalah$f'(x)=0$

Contoh:$\begin{aligned} f(x)&=2 &\rightarrow f'(x)=0\\ f(x)&=13 &\rightarrow f'(x)=0\\ f(x)&=100 &\rightarrow f'(x)=0 \end{aligned}$

2. Jika $f(x)=cx$, maka turunannya adalah$f'(x)=c$

Contoh:$\begin{aligned} f(x)&=2x &\rightarrow &f'(x)=2\\ f(x)&=13x &\rightarrow &f'(x)=13\\ f(x)&=100x &\rightarrow &f'(x)=100 \end{aligned}$

3. Jika $f(x)=x^n$ maka turunannya adalah$f'(x)=nx^{n-1}$

Contoh:$\begin{aligned} f(x)&=x^4 &\rightarrow &f'(x)=4x^3\\ f(x)&=x^3 &\rightarrow &f'(x)=3x^2\\ f(x)&=x^2 &\rightarrow &f'(x)=2x \end{aligned}$

4. Jika $f(x)=cx^n$maka turunannya adalah$f'(x)=cnx^{n-1}$

Contoh:$\begin{aligned} f(x)&=2x^4 &\rightarrow &f'(x)=8x^3\\ f(x)&=13x^3 &\rightarrow &f'(x)=39x^2\\ f(x)&=100x^2 &\rightarrow &f'(x)=200x \end{aligned}$

5. Jika $f(x)=c\,u(x)$ maka turunannya adalah$f'(x)=c\,u'(x)$

Contoh:$\begin{aligned} f(x)&=4\ln{x}&\rightarrow &f'(x)=4\frac{1}{x}\\ f(x)&=3\cos{x}&\rightarrow &f'(x)=3\sin{x}\\ f(x)&=2\sin{x}&\rightarrow &f'(x)=-2\cos{x} \end{aligned}$

6. Jika $f(x)=u(x)\pm v(x)$ maka turunannya adalah$f'(x)=u'(x)\pm v'(x)$

Contoh:$\begin{aligned} f(x)&=2x+x^2&\rightarrow &f'(x)=2+2x\\ f(x)&=x^4-x^3&\rightarrow &f'(x)=4x^3-3x^2\\ f(x)&=\sin{x}+\cos{x}&\rightarrow &f'(x)=\cos{x}-\sin{x} \end{aligned}$

7. Jika $f(x)=u(x)v(x)$ maka turunannya adalah$f'(x)=u'(x)v(x)+u(x)v'(x)$

Contoh:$f(x)=x^4x^3$Misalkan $u(x)=x^4$ dan $v(x)=x^3,$ maka $u'(x)=4x^3$ dan $v'(x)=3x^2,$ sehingga$\begin{aligned} f'(x)&=(4x^3)(x^3)+(x^4)(3x^2)\\ &=4x^6+3x^6\\ &=7x^6 \end{aligned}$

8. Jika $f(x)=\displaystyle\frac{u(x)}{v(x)}$ maka turunannya adalah$f'(x)=\frac{u'(x)v(x)-u(x)v'(x)}{(v(x))^2}$

Contoh:$f(x)=\frac{x^4}{x^3}$Misalkan $u(x)=x^4$ dan $v(x)=x^3,$ maka $u'(x)=4x^3$ dan $v'(x)=3x^2,$ sehingga$\begin{aligned} f'(x)&=\frac{(4x^3)(x^3)-(x^4)(3x^2)}{(x^3)^2}\\ &=\frac{4x^6-3x^6}{x^6}\\ &=1 \end{aligned}$

9. Jika $f(x)={u(x)}^n$ maka turunannya adalah$f'(x)=n(u(x))^{n-1}u'(x)$

Contoh:$f(x)=(2x+x^2)^4$Misalkan $u(x)=2x+x^2,$ sehingga $u'(x)=2+2x,$ maka$f'(x)=4\left(2x+x^2\right)^3(2+2x)$
CONTOH SOAL TURUNAN

Contoh Soal Turunan Beserta Pembahasannya

Soal No. 1
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 3x⁴ + 2x² − 5x
b) f(x) = 2x³ + 7x

Pembahasan
Rumus turunan fungsi aljabar bentuk axⁿ

Sehingga:
a) f(x) = 3x⁴ + 2x² − 5x
f '(x) = 4⋅3x^{4− 1} + 2⋅2x²⁻¹ − 5x^1-1
f '(x) = 12x³ + 4x¹ − 5x⁰
f '(x) = 12x³ + 4x − 5

b) f(x) = 2x³ + 7x
f '(x) = 6x² + 7

Soal No. 2
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 10x
b) f(x) = 8
c) f(x) = 12

Pembahasan
a) f(x) = 10x
f(x) = 10x¹
f '(x) = 10x¹⁻¹
f '(x) = 10x⁰
f '(x) = 10



b) f(x) = 8
f(x) = 8x⁰
f '(x) = 0⋅ 8x⁰⁻¹
f '(x) = 0



c) f(x) = 12
f '(x) = 0

Soal No. 3
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 5(2x² + 4x)
b) f(x) = (2x + 3)(5x + 4)

Pembahasan
Tentukan turunan pertama dari fungsi berikut:
a) f(x) = 5(2x² + 4x)
f(x) = 10x² + 20x
f ' (x) = 20x + 20

b) f(x) = (2x + 3)(5x + 4)

Urai terlebih dahulu hingga menjadi
f (x) = 10x² + 8x + 15x + 12
f (x) = 10x² + 13x + 12

Sehingga
f ' (x) = 20x + 13

Soal No. 4
Tentukan turunan dari fungsi-fungsi berikut

a)
b)
c)

Pembahasan

a)
b)
c)

Soal No. 5
Tentukan turunan dari fungsi-fungsi berikut, nyatakan hasil akhir dalam bentuk akar

a)
b)
c)

Pembahasan

a)
b)
c)

Soal No. 6
Dengan menggunakan rumus turunan hasil kali fungsi berikut ini



Tentukan turunan untuk f(x) = (x² + 2x + 3)(4x + 5)

Pembahasan
Misal :
u = (x² + 2x + 3)
v = (4x + 5)

maka
u ' = 2x + 2
v ' = 4

sehingga penerapan rumus di atas menjadi

Soal No. 7
Tentukan turunan dari f(x) = (2x + 1)4

Jawab:

Misalnya:

u(x) = 2x + 1  ⇒  u'(x) = 2
n = 4
f ‘(x) = n[u(x)]n-1 . u'(x)
f ‘(x) = 4(2x + 1)4-1 . 2
f ‘(x) = 8(2x + 1)3 

 

Soal No. 8
Tentukan turunan dari y = (x2 − 3x)7

Jawab :

y’ = 7(x2 − 3x)7-1 . (2x − 3)
y’ = (14x − 21) . (x2 − 3x)6

Soal No. 9

Tentukanlah turunan fungsi dari f(x) = 2x(x4 – 5).

Jawab:

Misalkan jika u(x) = 2x dan v(x) = x4 – 5, maka:

u‘ (x) = 2 dan v‘ (x) maka = 4x3

Dengan begitu, akan didapatkan penjabaran serta hasilnya:

f ‘(x) = u ‘(x).v(x) + u(x).v ’(x) = 2(x4 – 5) + 2x(4x3 ) = 2x4 – 10 + 8x4 = 10x4 – 10

Soal no. 10 

1. Tentukan turunan pertama dari fungsi f(x) = x3 – 2x2 + 3x !

Pembahasan

f’(x) = 3.1.x3-1 – 2.2x2-1 + 1.3.x1-1

f’(x) = 3x2 – 4x + 3

Jadi, turunan pertama dari fungsi f(x) = x3 – 2x2 + 3x adalah f’(x) 3x2 – 4x + 3.

2. Carilah turunan pertama dari fungsi f(x) = (3x + 2)(2x + 5) !

Pembahasan

f(x) = (3x + 2)(2x + 5)

f(x) = 3x.2x + 3x.5 + 2.2x + 2.5

f(x) = 6x2 + 15x + 4x + 10

f(x) = 6x2 + 19x + 10

f’(x) = 2.6.x2-1 + 1.19.x1-1 + 0.10.x0-1

f’(x) = 12x + 19 + 0

f’(x) = 12x + 19

Jadi turunan pertama dari fungsi f(x) = (3x + 2)(2x + 5) adalah f’(x) = 12x + 19 + 0 .

3. Hitunglah turunan pertama dari fungsi f(x) = 4x½ !

Pembahasan

f’(x) = ½.4.x½-1

f’(x) = 2x-½

Jadi turunan pertama dari fungsi f(x) = 4x½ adalah f’(x) = 2x-½ .

4. Berapakah turunan pertama dari fungsi f(x) = 4 √x3 ?

Pembahasan

f(x) = 4 √x

f(x) = 4 x3/2

f’(x) = 3/2.4.x3/2 – 1

f’(x) = 6x½

f’(x) = 6 √x

Jadi, turunan pertama dari fungsi f(x) = 4 √x3 adalah f’(x) = 6 √x.

5. Tentukan turunan pertama dari fungsi f(x) = (x2 + 3x + 4)(2x + 3).

Pembahasan

f(x) = (x2 + 3x + 4)(2x + 3)

Misal:

u = x2 + 3x + 4

v = 2x + 3

Maka:

u’ = 2x + 3

v’ = 2

Sehingga:

f’(x) = u’v + uv’

f’(x) = (2x + 3)(2x + 3) + (x2 + 3x + 4).2

f’(x) = 4x2 + 12x + 9 + 2x2 + 6x + 8

f’(x) = 6x2 + 18x + 17

Jadi, turunan dari f(x) = (x2 + 3x + 4)(2x + 3) adalah f’(x) = 6x2 + 18x + 17.

6. Carilah turunan pertama dari f(x) = (x3+4) / (2x+3) !

Pembahasan

Misal:

u = x3+4

v = 2x+3

Maka:

u’ = 3x2

v’ = 2

Sehingga

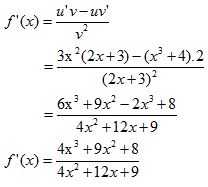
Jadi,  turunan pertama dari f(x) = (x3+4) / (2x+3) adalah f’(x) = (4x3 + 9x2 + 8) / (4x2 + 12x + 9).

7. Hitunglah turunan pertama dari f(x) = sin x . cos x !

Pembahasan

Misal:

u = sin x

v = cos x

Maka:

u’ = cos x

v’ = – sin x

Sehingga:

f’(x) = u’v + uv’

f’(x) = cos x cos x + sin x (-sin x)

f’(x) = cos2 x – sin2 x

f’(x) = cos 2x (identitas trigonometri)

Jadi turunan pertama dari f(x) = sin x . cos x adalah f’(x) = cos 2x.