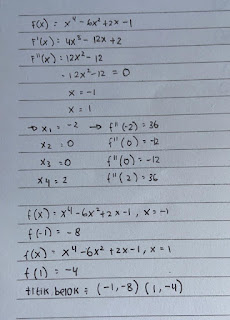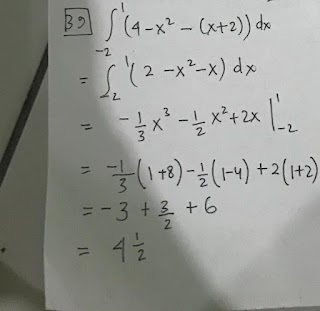Pendapat tentang Pembelajaran Jarak Jauh (PJJ)

jawaban soal uas

 Nasywa Kayla Zahra (27)

XI IPS 2

Assalamualaikum Wr.Wb

1. p = 1

2. 1/32 

3. m<n =0

4. 0

5. -2

6. 63/25

7. 2x+y-2 = 0

8. (-1,8)

9. (2,-79)

10. tak terhingga

11. naik x > 4, turun 2 > x > 4

12. pernyataan 3&4 pada soal salaah

13. ab = 2

14. Rp 391.000

15.P= 2 ∛2

L= 2 ∛2

t= ∛2

16.1/3

17. -9/2

18. 1/5 (x⁴-1)⁵ + C

19. 20 5/6

20. 208⅓π 

21. √2 + √7

22. √2/4

23. 4/5

24. 4/3

25. -1/6

26. f(x) = (4x - 21 (x2 - 27) 6 + (6x2 + 6x + 4) > disarankan penulisannya liat foto asli

27. y = 6x + 12, y = -6x = 12, y = -12x - 18 dan y = 12x - 18

28. naik pada 1 < x < 5 

29. (-1,-8) (1,-4) 

30. -36

31. 1 dan -4

32.  Interval naik 1<x<5

Interval turun x<1 atau x>5

33. y = 12x - 29

34. 40.000

35. 32.000 Jiwa

36. 5 ⁵√(x³ + 2x -1)²

37. -3 

38. 62/3

39. 4 ½

40. 16/3 phi (sat.volume)

No 1.

No 2

No 3

No 4

No 5

No 6

No 7

No 8

No 9

No 10

No 11

No 12

No 13

No 14

No 15

No 16

No 17

No 18

No 19

No 20

No 21

No 22

No 23

No 24

No 25

No 26

No 27

No 28

No 29

No 31

No 32

No 33

No 34

No 35

No 36

No 37

No 38

No 39

No 40

SOAL Limit, Turunan, Integral

 Nasywa Kayla Zahra (27) 

XI IPS 2

Assalamualaikum Wr.Wb

SOAL Limit, Turunan, Integral

Carilah gradien garis singgung kurva f(x) = 5x² – 8x + 4 di titik(2, 8) ?

Pembahasan

Titik singgung dititik (2, 8), maka x₁ = 2
Dengan demikian, gradien garis adalah : m = f’(x1)
m = 10x1 – 8
m = 10(2) – 8
m = 12

Soal No.2

---

Tentukanlah persamaan garis singgung untuk kurva y = x² + 2x di titik (1,3)

Pembahasan

f(x) = x2 + 2x
f'(x) = 2x + 2
m = f '(1) = 2(1) + 2 = 4
m = 4

Jadi, persamaan garis singgungnya adalah :
y – y₁ = m(x – x₁)
y − 3 = 4(x − 1)
y − 3 = 4x − 4
y = 4x − 1

Soal No.3

---

Tentukanlah Persamaan garis singgung kurva y = 2x - 3x² di titik dengan absis 2

Pembahasan

Absis itu adalah sumbu-x, jadi x =2:
Langkah 1 : Cari titik singgung dengan memasukkan nilai x = 2
y = 2x - 3x²
y = 2(2) − 3(2)²
y = −8
Jadi titik singgung : (2, −8)

Langkah 2: Cari nilai gradien
f(x) = 2x − 3x²
f '(x) = 2 − 6x
m = f '(2) = 2 − 6(2) = −10
m = −10

Jadi, persamaan garis singgungnya adalah :
y – y₁ = m(x – x₁)
y − (−8) = −10(x − 2)
y + 8 = −10x + 20
y = −10x + 12

Soal No.4

---

Tentukanlah Persamaan garis singgung kurva y = 2x³ - 4x² di titik berabsis 2

Pembahasan

Absis itu adalah sumbu-x, jadi x =2:
Langkah 1 : Cari titik singgung dengan memasukkan nilai x = 2
y = 2x³ - 4x²
y = 2(2)³ − 4(2)²
y = 16 - 16
y = 0
Jadi titik singgung : (2, 0)

Langkah 2: Cari nilai gradien
f(x) = 2x³ - 4x²
f '(x) = 6x² - 8x
m = f '(2) = 6(2)² − 8(2)
m = 24 - 16
m = 8

Jadi, persamaan garis singgungnya adalah :
y – y₁ = m(x – x₁)
y − 0 = 8(x − 2)
y = 8x - 16

Soal No.5

---

Tentukanlah Persamaan garis singgung kurva y = x² di titik berabsis -2

Pembahasan

Absis itu adalah sumbu-x, jadi x = -2:

Langkah 1 : Cari titik singgung dengan memasukkan nilai x = -2
y = x²
y = (-2)²
y = 4
Jadi titik singgung : (-2, 4)

Langkah 2: Cari nilai gradien
f(x) = x²
f '(x) = 2x
m = f '(-2) = 2(-2)
m = -4

Jadi, persamaan garis singgungnya adalah :
y – y₁ = m(x – x₁)
y − 4 = -4(x − (-2))
y - 4 = -4x - 8
y = -4x - 4

Soal No.6

---

Tentukanlah persamaan garis singgung untuk kurva y = 3 + 2x - x² sejajar dengan garis 4x + y = 3

Pembahasan

Langkah 1 : Cari nilai m₁
y = 3 + 2x - x²
m₁ = f'(x) = -2x + 2
m₁ = -2x + 2

Langkah 2 : Cari nilai m₂
4x + y = 3
y = -4x + 3
m₂ = -4 (Inga !! Jika y = ax + b ⇒ m = a )

Langkah 3 : Cari nilai x
Karena kedua garis saling sejajar maka berlaku :
m₁ = m₂
-2x + 2 = -4
-2x = -6
x = 3
Langkah 4 : Cari nilai y dengan memasukkan nilai x = 3
y = 3 + 2x - x²
y = 3 + 2(3) - 3²
y = 3 + 6 - 9
y = 0

Sekarang kita telah memiliki titik singgung (3,0)

Langkah 4: Persamaan garis singgung
y – y₁ = m(x – x₁)
y - 0 = -4(x - 3)
y = -4x + 12

Soal No.7

---

Carilah persamaan garis singgung pada kurva y = x³ + 10 di titik yang berordinat 18 ?

Pembahasan

Ordinat itu adalah sumbu-y, jadi y = 18

Langkah 1 : Cari titik singgung dengan memasukkan nilai y = 18
y = x³ + 10
18 = x³ + 10
x³ = 18 - 10
x³ = 8
x = 2
Jadi titik singgung : (2,18)

Langkah 2: Cari nilai gradien
f(x) = x³ + 10
f'(x) = 3x²
m = f'(2) = 3(2)²
m = 12

Jadi,Persamaan garis singgungnya adalah y – y₁ = m(x – x₁)
y - 18 = 12(x - 2)
y - 8 = 12x - 24
y = 12x - 16

Soal No.8

---

Carilah persamaan garis singgung pada kurva y = x² - x + 3 di titik yang berordinat 5 ?

Pembahasan

Ordinat itu adalah sumbu-y, jadi y = 5

Langkah 1 : Cari titik singgung dengan memasukkan nilai y = 5
y = x² - x + 3
5 = x² - x + 3
x² - x + 3 - 5 = 0
x² - x - 2 = 0
(x - 2)(x + 1) = 0
x = 2 atau x = -1
Jadi terdapat dua titik singgung : (2,5) atau (-1,5)

Langkah 2: Cari nilai gradien
Nilai gradien untuk x = 2
f(x) = x² - x + 3
f'(x) = 2x - 1
m = f'(2) = 2(2) - 1
m = 3

Nilai gradien untuk x = -1
f(x) = x² - x + 3
f'(x) = 2x - 1
m = f'(-1) = 2(-1) - 1
m = -3

Langkah 3: Menentukan persamaan garis singgung
Karena kita memiliki dua titik singgung, tentunya akan ada dua persamaan garis singgung

Persamaan garis singgungnya untuk titik (2,5) dengan m = 3
y – y₁ = m(x – x₁)
y - 5 = 3(x - 2)
y = 3x - 6 + 5
y = 3x - 1

Persamaan garis singgungnya untuk titik (-1,5) dengan m = -3
y – y₁ = m(x – x₁)
y - 5 = -3(x - (-1))
y - 5 = -3x - 3
y = -3x + 2

Jadi, ada dua persamaan garis singgung, yaitu y = 3x - 1 atau y = -3x + 2

Soal No.9

---

Carilah persamaan garis singgung pada kurva y = x² - 5x + 6 jika gradien garis singgungnya adalah 3 ?

Pembahasan

Langkah 1: Cari titik singgungnya
f(x) = x² - 5x + 6
f'(x) = 2x - 5
m = f'(x)
3 = 2x - 5
2x = 3 + 5
x = 4

y = x² - 5x + 6
y = 4² - 5(4) + 6
y = 16 - 20 + 6
y = 2

Jadi titik singgung : (4,2)

Langkah 2: Menentukan persamaan garis singgung
y – y₁ = m(x – x₁)
y - 2 = 3(x - 4)
y - 2 = 3x - 12
y = 3x - 10

Soal No.10

---

Tentukanlah persamaan garis singgung kurva y = x³ - 3x² - 5x + 10 jika gradien garis singgungnya adalah 4 ?

Pembahasan

Langkah 1: Cari titik singgungnya f(x) = x³ - 3x² - 5x + 10
f'(x) = 3x² - 6x - 5
m = f'(x)
4 = 3x² - 6x - 5
3x² - 6x - 9 = 0 (lalu kita bagi 3)
x² - 2x - 3 = 0
(x - 3)(x + 2) = 0
x = 3 atau x = -2

Untuk x = 3
y = x³ - 3x² - 5x + 10
y = 3³ - 3(3)² - 5(3) + 10
y = 27 -27 - 15 + 10
y = -5
Titik singgung pertama (3,-5)

Untuk x = -2
y = x³ - 3x² - 5x + 10
y = (-2)³ - 3(-2)² - 5(-2) + 10
y = -8 - 12 + 10 + 10
y = 0
Titik singgung kedua (-2,0)

Langkah 2: Menentukan persamaan garis singgung
Untuk titik singgung pertama (3,-5)
y – y₁ = m(x – x₁)
y – (-5) = 4(x – 3)
y + 5 = 4x -12
y = 4x -17

Untuk titik singgung kedua (-2,0)
y – y₁ = m(x – x₁)
y – 0 = 4(x – (-2))
y = 4x + 8

Jadi ada dua persamaan garis singgung yaitu :
y = 4x -17 dan y = 4x + 8

Soal No.11

---

Tentukanlah persamaan garis singgung kurva y = 3 - x² yang tegak lurus terhadap garis 4y = x + 1 ?

Pembahasan

Langkah 1 : Cari nilai m₁
y = 3 - x²
m₁ = f'(x) = -2x
m₁ = -2x

Langkah 2 : Cari nilai m₂
4y = x + 1
y = 

14

x + 

14

m₂ = 

14

(Ingat !! Jika y = ax + b ⇒ m = a)

Langkah 3 : Cari nilai x
Karena kedua garis tegak lurus maka berlaku :
m₁ . m₂ = -1
m₁ . 

14

 = -1
m₁ = -4

Masukkan nilai m₁ ke dalam persamaan langkah-1 :
m₁ = -2x
-4 = -2x
x = 2

Langkah 4 : Cari nilai y dengan memasukkan nilai x = 2
y = 3 - x²
y = 3 - 2²
y = 3 - 4
y = -1
Jadi titik singgungnya : (2,-1)

Langkah 5 : Menentukan persamaan garis singgung
y - y₁ = m(x - x₁)
y - (-1) = -4(x - 2)
y + 1 = -4x + 8
y = -4x + 7

Jadi persamaan garis singgungnya : y = -4x + 7

Soal No.12

---

Persamaan garis menyinggung kurva y = x² - 3x - 4 di titik (4,0) adalah .....
a. y = 5x + 20
b. y = 5x - 20
c. y = -5x + 20
d. y = -5x - 20

Pembahasan

y = x² - 3x - 4
y' = 2x - 3
m = y '(4) = 2(4) - 3 = 5
m = 5

Jadi, persamaan garis singgungnya adalah :
y – y₁ = m(x – x₁)
y - 0 = 5 (x - 4)
y = 5x - 20

Jawab c:

Soal No.13

---

Tentukan gradien garis dengan persamaan berikut :
1.) y = 2x - 8
2.) 4x - 2y + 6 = 0
3.) 3y = 6x - 1
4.) 7x - 14y + 2 = 0

Pembahasan

1.) Untuk Persamaan : y = 2x - 8

Jika persamaan y = ax + b ⇒ m = a
y = 2x - 8
m = 2

2.) Untuk Persamaan : 4x - 2y + 6 = 0

Jika persamaan ax + by = c ⇒ m = -

ab

4x - 2y + 6 = 0
m = -

4-2

m = -(-2)
m = 2

3.) Untuk Persamaan : 3y = 6x - 1

Jika persamaan ax + by = c ⇒ m = -

ab

3y = 6x - 1
6x - 3y - 1 = 0
m = -

6-3

m = -(-2)
m = 2

4.) Untuk Persamaan : 7x - 14y + 2 = 0

Jika persamaan ax + by = c ⇒ m = -

ab

7x - 14y + 2 = 0
m = -

7-14

m = -

1-2

m = 

12

Soal Latihan Turunan dan Garis Singgung

 Assalamualaikum Wr.Wb

Nasywa Kayla Zahra (27) XI IPS 2 

Matematika Soal Latihan No. 7

 

 

Jadi persamaan garis singgungnya adalah y = -2x + 2.

Persamaan garis adalah sebuah metode pada matematika. Digunakan untuk mendefinisikan sebuah garis lurus ke dalam sebuah persamaan.  Bentuk umum persamaan garis lurus dinyatakan dalam persamaan y = mx + c, dengan m adalah gradien, x merupakan variabel, dan c adalah konstanta    

Jika diketahui dua koordinat, gradien dapat dicari dengan menggunakan rumus m = . Suatu ruas garis dikatakan tegak lurus jika m1.m2 = -1 . Suatu ruas garis dikatakan sejajar jika m1 = m2   .

Jika gradien dan titik pada garis diketahui, persamaan garis dapat ditentukan dengan rumus y - y₁ = m(x - x₁)

 

 

Pembahasan

y = x² - 4x + 3

 

y' = 2x - 4

 

x - 2y + 8 = 0​

 

2y = x + 8

 

y = 1/2x + 4

 

Garis ini memiliki gradien 1/2

 

Karena garis singgungnya tegak lurus dengan garis ini maka

 

m1.m2 = -1

 

1/2 . m2 = -1

 

m2 = -2

 

m2 ini adalah gradien garis singgung, sehingga sama dengan turunan

 

y' = -2

 

-2 = 2x - 4

 

2x = 2

 

x = 1

 

y = x² - 4x + 3

 

y = 1 - 4 + 3

 

y = 0

 

maka persamaan garis singgungnya

 

y – y1 = m(x – x1)

 

y - 0 = -2(x - 1)

 

y = -2x + 2

 

Jadi persamaan garis singgungnya adalah y = -2x + 2

 

Gambar dapat dilihat pada lampiran. Warna merah adalah y=x²-4x+3, warna biru adalah x -2y + 8= 0​ dan warna hijau adalah y = -2x + 2

 

 

Luas dan Volume Daerah yang Berkaitan dengan Integral Bersama Contoh Soalnya

 Nasywa Kayla Zahra (27) XI IPS 2 

Assalamualaikum Wr.Wb

LUAS DAERAH

Misalkan y = fx berharga positif pada daerah latexa≤x≤b dan kontinu pada daerah tersebut, maka luas daerah yang dibatasi oleh grafik y = fx dengan sumbu x dari x = a ke x = b adalah

Bila y = fx berharga negatif pada daerah latexa≤x≤b maka luas daerah yang dibatasi oleh y = fx dengan semubu x dari x = a ke x = b adalah

Misalkan latexf(x)≥g(x)$latexf(x)\ge g(x)$ pada daerah latexa≤x≤b$latexa\le x\le b$ maka luas daerah yang dibatasi oleh grafik y = fx$x$ dan y = gx$x$ adalah

Contoh 1 :

Tentukan luas daerah yang dibatasi oleh grafik y = x2 + 2x dengan sumbu x

Jawab :

Contoh 2 :

Tentukan luas daerah yang dibatasi oleh grafik y = x2 dengan garis y = x + 8

Jawab :

 

y = x2 ……… 1$1$

y = x + 6 ……… 2$2$

Dari 1$1$ dan 2$2$ didapat

x2 = x + 6

x2 – x – 6 = 0

x1 = 3 ; x2 = 2

Luas daerah,

latexL=∫(x+6−x2)dx=12x2+6x−13x3∣3−2$latexL=\int \left(x+6-x^2\right)dx=\frac{1}{2}{x}^2+6x-\frac{1}{3}{x}^3{\mid }_{-2}^3$

latex=(92+18−9)−(2−12+83)=2112$latex=(\frac{9}{2}+18-9)-(2-12+\frac{8}{3})=21\frac{1}{2}$

ISI BENDA PUTAR

Misalkan y = fx$x$ terdefinisi dan integrabel pada daerah latexa≤x≤b$latexa\le x\le b$ , bila daerah yang dibatasi oleh y = fx$x$ dan sumbu x dari x = a ke x = b diputar mengelilingi sumbu x, maka isi benda putar yang terjadi adalah :

Contoh 1:

Tentukan isi benda putar bila daerah yang dibatasi oleh grafik y = x2 dari x = 0 ke x =1 diputar mengeliling sumbu x

Jawab :

Isi benda putar yang terjadi

Contoh 2 :

Tentukan isi benda putar bila daerah yang dibatasi oleh grafik y = x2 dan garis y = x + 2 diputar mengeliling sumbu x

Jawab :

Batas integral

latexy=x2$latexy=x^2$

latexy=x+2$latexy=x+2$

Sehingga :

latexx2=x+2$latex{x}^2=x+2$

Daftar pustaka : https://ilmuhitung.com/aplikasi-integral-menentukan-luas-dan-volume-suatu-daerah/

Luas dan Volume Daerah yang Berkaitan dengan Integral Bersama Contoh Soalnya 

Integral bisa diaplikasikan dalam kehidupan sehari-hari. Salah satu contoh yang umum dikenal adalah luas daerah. Luas daerah yang dimaksud adalah luas daerah di bawah kurva. Adapun langkah menghitungnya adalah sebagai berikut.

• Batas daerah yang akan diintegralkan harus jelas. Adapun batas daerah yang dimaksud adalah batas kiri dan kanannya serta batas atas dan bawahnya. Bentuk batas daerah bisa berupa fungsi atau konstanta, fungsi linier dan nonlinier (kuadrat, pangkat 3, akar pangkat). Bagaimana jika salah satu batas belum diketahui? maka harus mencarinya terlebih dahulu, agar luasnya bisa dihitung.
• Harus mampu menggambar daerah di dalam kurva sesuai dengan batas-batas yang telah ditentukan (jika gambar masih dinyatakan dalam batas-batasnya saja). Oleh karena itu, diperlukan kemampuan untuk menggambar dengan baik.
• Setelah itu juga harus bisa menempatkan rumus yang tepat untuk menghitung luas daerah berdasarkan ketentuan yang telah ada. Jangan lupa untuk memperhatikan gambar daerah dan rumus yang bersesuaian. 

a) Bentuk daerah jenis 1

b) Bentuk daerah jenis 2

Volume Benda Putar

.

Contoh Soal

1. Luas daerah yang dibatasi oleh kurva 

$y=x^2+4x+6$ dan garis $y=2-x$ adalah $\cdots$ satuan luas.
A. $\frac{27}{2}$                 C. $\frac{9}{2}$               E. $\frac{1}{2}$
B. $\frac{9}{4}$                   D. $\frac{3}{2}$

Pembahasan :

Gambarkan sketsa grafik dari fungsi $y=x^2+4x+6$ dan $y=2-x$ pada bidang Kartesius.
Daerah yang diarsir merupakan daerah yang akan kita hitung luasnya. Daerah tersebut terbatas pada selang titik potong kedua kurva. Untuk itu, kita akan mencari koordinat titik potongnya dulu dengan cara menyamakan kedua fungsi.
$\begin{array}{cc}y& =y\\ x^2+4x+6& =2-x\\ x^2+5x+4& =0\\ (x+4)(x+1)& =0\end{array}$
Diperoleh $x=-4$ atau $x=-1$.
Untuk $x=-4$, diperoleh $y=6$.
Untuk $x=-1$, diperoleh $y=3$.
Jadi, koordinat titik potongnya adalah $(-4,6)$ dan $(-1,3)$.
Karena variabel integralnya menggunakan $x$, maka kita beri batas atas dan batas bawah integral berdasarkan absis titik potong, yaitu $x=-4$ sebagai batas bawah dan $x=-1$ sebagai batas atas.
Perhatikan bahwa kurva $y=2-x$ selalu berada di atas kurva $y=x^2+4x+6$ pada interval $-4<x<-1$ sehingga luas daerah yang diarsir dinyatakan oleh
$$\begin{array}{cc}L& ={\int }_{-4}^{-1}(y_{\text{atas}}-y_{\text{bawah}})\text{d}x\\ & ={\int }_{-4}^{-1}\left(\right(2-x)-(x^2+4x+6)\text{d}x\\ & ={\int }_{-4}^{-1}(-x^2-5x-4)\text{d}x\\ & ={[-\frac{1}{3}{x}^3-\frac{5}{2}{x}^2-4x]}_{-4}^{-1}\\ & =(-\frac{1}{3}(-1{)}^3-\frac{5}{2}(-1{)}^2-4(-1\left)\right)-(-\frac{1}{3}(-4{)}^3-\frac{5}{2}(-4{)}^2-4(-4\left)\right)\\ & =(\frac{1}{3}-\frac{5}{2}+4)-(\frac{64}{3}-40+16)\\ & =\frac{11}{6}+\frac{8}{3}=\frac{27}{6}=\frac{9}{2}\end{array}$$

2. Perhatikan gambar berikut.

Luas daerah yang diarsir adalah $\cdots$ satuan luas.
A. $\frac{7}{2}$                   C. $\frac{11}{2}$                E. $3$
B. $\frac{9}{2}$                   D. $\frac{9}{5}$

Pembahasan :

Daerah yang diarsir terbatas pada selang titik potong kedua kurva.
Untuk itu, kita akan mencari koordinat titik potongnya dulu dengan cara menyamakan kedua fungsi.
$\begin{array}{cc}y& =y\\ x^2& =2-x\\ x^2+x-2& =0\\ (x+2)(x-1)& =0\end{array}$
Diperoleh $x=-2$ atau $x=1$.
Untuk $x=-2$, diperoleh $y=4$.
Untuk $x=1$, diperoleh $y=1$.
Jadi, koordinat titik potongnya adalah $(-2,4)$ dan $(1,1)$.
Karena variabel integralnya menggunakan $x$, maka kita beri batas atas dan batas bawah integral berdasarkan absis titik potong, yaitu $x=-2$ sebagai batas bawah dan $x=1$ sebagai batas atas.
Perhatikan bahwa kurva $y=2-x$ selalu berada di atas kurva $y=x^2$ pada interval $-2<x<1$ sehingga luas daerah yang diarsir dinyatakan oleh
$$\begin{array}{cc}L& {\int }_{-2}^1(y_{\text{atas}}-y_{\text{bawah}})\text{d}x\\ & ={\int }_{-2}^1\left(\right(2-x)-(x^2\left)\right)\text{d}x\\ & ={\int }_{-2}^1(-x^2-x+2)\text{d}x\\ & ={[-\frac{1}{3}{x}^3-\frac{1}{2}{x}^2+2x]}_{-2}^1\\ & =(-\frac{1}{3}(1{)}^3-\frac{1}{2}(1{)}^2+2(1\left)\right)-(-\frac{1}{3}(-2{)}^3-\frac{1}{2}(-2{)}^2+2(-2\left)\right)\\ & =(-\frac{1}{3}-\frac{1}{2}+2)-(\frac{8}{3}-2-4)\\ & =\frac{7}{6}-(-\frac{10}{3})=\frac{27}{6}=\frac{9}{2}\end{array}$$

3. Sebuah daerah yang dibatasi oleh kurva 

$y=x^2+a$, garis $y=-x+a$, dan garis $x=a$ mempunyai luas $\frac{1}{3}a$. Nilai dari $10a$ adalah $\cdots \cdot$
A. $1$                     C. $10$                     E. $20$
B. $5$                     D. $15$

Pembahasan : 

Karena $L=\frac{1}{3}a$, maka kita simpulkan bahwa $a>0$.
Sketsa kurva $y=x^2+a$ yang merupakan pergeseran kurva $y=x^2$ ke atas sehingga titik puncaknya di $(0,a)$.
Sketsa kurva $y=-x+a\iff x+y=a$ yang merupakan garis lurus dengan perpotongan terhadap sumbu-$X$ di $(a,0)$ dan perpotongan terhadap sumbu-$Y$ di $(0,a)$.
Sketsa kurva $x=a$ berupa garis tegak.

Daerah yang diarsir dibatasi oleh ketiga kurva tersebut pada selang $(0,a)$.
Perhatikan bahwa pada selang itu, kurva $y=x^2+a$ selalu berada di atas kurva $y=-x+a$ sehingga luas daerah yang diarsir ditentukan oleh integral tentu berikut.
$\begin{array}{cc}L& ={\int }_0^a\left[\right(x^2+a)-(-x+a\left)\right]\text{d}x\\ & ={\int }_0^a(x^2+x)\text{d}x\\ & ={[\frac{1}{3}{x}^3+\frac{1}{2}{x}^2]}_0^a\\ & =(\frac{1}{3}{a}^3+\frac{1}{2}{a}^2)-0\\ & =\frac{a^3}{3}+\frac{a^2}{2}\end{array}$
Karena diketahui luasnya $\frac{1}{3}a$, maka diperoleh persamaan
$\begin{array}{cc}\frac{a^3}{3}+\frac{a^2}{2}& =\frac{1}{3}a\\ \text{Kalikan}6\text{di kedua}& \text{ruas}\\ 2a^3-3a^2& =2a\\ 2a^3+3a^2-2a& =0\\ a(2a^2+3a-2)& =0\\ a(2a+4)(2a-1)& =0\end{array}$
Diperoleh $a=0$ atau $a=-2$ atau $a=\frac{1}{2}$. Karena $a$ harus positif, maka dipilih $a=\frac{1}{2}$.
Dengan demikian, nilai $10a=10\cdot \frac{1}{2}=5$

4. Volume benda putar yang terbentuk jika daerah yang dibatasi oleh kurva 

$x-y^2+1=0$, $-1\le x\le 4$, dan sumbu-$X$, diputar mengelilingi sumbu-$X$ sejauh ${360}^{\circ }$ adalah $\cdots$ satuan volume.
A. $8\frac{1}{2}\pi$                    D. $12\frac{1}{2}\pi$
B. $9\frac{1}{2}\pi$                    E. $13\frac{1}{2}\pi$
C. $11\frac{1}{2}\pi$

Pembahasan : 

Kurva $x-y^2+1=0$ dapat ditulis menjadi $y^2=x+1$. Bila kita gambar kurvanya yang berupa parabola terbuka ke kanan, beserta garis tegak $x=-1$ dan $x=4$, kita akan memperoleh gambar seperti berikut.
Daerah yang diarsir merupakan daerah yang dibatasi oleh kurva tersebut dan sumbu-$X$ pada selang $[-1,4]$.
Bila diputar mengelilingi sumbu-$X$ sejauh ${360}^{\circ }$, maka kita peroleh
$$\begin{array}{cc}V& =\pi {\int }_{-1}^4{y}^2\text{d}x\\ & =\pi {\int }_{-1}^4(x+1)\text{d}x\\ & =\pi {[\frac{1}{2}{x}^2+x]}_{-1}^4\\ & =\pi [\left(\frac{1}{2}\right(4{)}^2+4)-\left(\frac{1}{2}\right(-1{)}^2+(-1))]\\ & =\pi \left[\right(8+4)-(\frac{1}{2}-1)]\\ & =\pi (12+\frac{1}{2})=12\frac{1}{2}\pi \end{array}$$Jadi, volume benda putar yang terbentuk adalah $12\frac{1}{2}\pi$ satuan volume.
(Jawaban D)

5. Volume benda dari daerah yang dibatasi oleh kurva 

$y=x^2$ dan garis $y=2x$ setelah diputar ${360}^{\circ }$ mengelilingi sumbu-$Y$ adalah $\cdots$ satuan volume.
A. $16\pi$                       D. $2\frac{2}{3}\pi$
B. $8\pi$                         E. $2\frac{1}{3}\pi$
C. $3\frac{2}{3}\pi$

Pembahasan : 

Gambarkan sketsa kurvanya terlebih dahulu seperti berikut.
Daerah yang diarsir merupakan daerah yang akan diputar terhadap sumbu-$Y$.
Daerah tersebut terbatas pada absis titik potong kedua kurva dan dapat ditentukan dengan menyamakan kedua fungsinya.
$\begin{array}{cc}y& =y\\ x^2& =2x\\ x^2-2x& =0\\ x(x-2)& =0\end{array}$
Diperoleh $x=0$ atau $x=2$.
Jadi, daerah arsir berada pada selang $[0,2]$.
[diputar terhadap sumbu-$Y$]
$y=x^2\iff x^2=y$
$y=2x\iff x=\frac{y}{2}\iff x^2=\frac{y^2}{4}$
Perhatikan bahwa pada selang tersebut, kurva $y=x^2$ selalu berada di atas kurva $y=2x$ (cara melihatnya: semakin ke kanan, artinya semakin ke atas) sehingga volume benda putar yang terbentuk dinyatakan sebagai berikut.
$\begin{array}{cc}V& =\pi {\int }_0^4(x_1^2-x_2^2)\text{d}y\\ & =\pi {\int }_0^4(y-\frac{y^2}{4})\text{d}y\\ & =\pi {[\frac{1}{2}{y}^2-\frac{1}{12}{y}^3]}_0^4\\ & =\pi \left[\frac{1}{2}\right(4^2-0^2)-\frac{1}{12}(4^3-0^3\left)\right]\\ & =\pi [8-5\frac{1}{3}]=2\frac{2}{3}\end{array}$
Jadi, volume benda putar yang terbentuk sebesar $2\frac{2}{3}$ satuan volume.
(Jawaban D)

Daftar Pustaka 

https://mathcyber1997.com/luas-daerah-integral/

https://mathcyber1997.com/soal-dan-pembahasan-volume-benda-putar-menggunakan-integral/

https://ahmadthohir1089.wordpress.com/2015/08/30/insyaallah-25/

https://www.quipper.com/id/blog/mapel/matematika/integral/