NILAI STASIONER, FUNGSI NAIK DAN FUNGSI TURUN

 Nasywa Kayla Zahra

XI IPS 2

27

Nilai Stasioner

1. Pengertian Nilai Stasioner Fungsi

Gambar 1. merupakan grafik fungsi f(x) = – (x – 1)² + 4. Turunan pertama dari fungsi f(x) = – (x – 1)² + 4 adalah f '(x) = –2(x – 1). Untuk x = 1, diperoleh f '(1) = –2(1 – 1) = 0. Oleh karena nilai f '(1) = 0 maka fungsi f(x) = –(x – 1)² + 4 mencapai nilai stasioner di x = 1 dengan nilai stasioner f(1) = – (1 – 1)² + 4 = 4. Selanjutnya, titik (1, 4) disebut titik stasioner.

Gambar 1. grafik fungsi f(x) = – (x – 1)² + 4.

Dari contoh di atas dapatkah Anda menduga pengertian nilai stasioner fungsi? Cobalah nyatakan dengan kata-kata Anda sendiri. Konsep nilai stasioner fungsi yang telah Anda pelajari tersebut merupakan hal khusus dari hal umum berikut.

Amati f "(x) > 0 untuk x < 0, dikatakan f cekung ke atas pada x < 0, f "(x) < 0 untuk 0 < x < 2, dikatakan f cekung ke bawah pada 0 < x < 2, dan f "(x) > 0 pada x > 2, dikatakan f cekung ke atas pada x > 2.

Di sekitar x = 0 (titik (0, 0)) terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah sehingga titik (0, 0) merupakan titik belok grafik fungsi f. Apakah titik (2, 0) merupakan titik belok? Bagaimana dengan titik (3, 0)? Dari uraian tersebut, dapatkah Anda menyatakan pengertian nilai stasioner fungsi? Cobalah nyatakan pengertian nilai stasioner fungsi dengan kata-kata Anda sendiri.

Definisi 1 :

Diketahui fungsi y = f(x) kontinu dan dapat diturunkan (diferentiable) di x = c. Fungsi y = f(x) memiliki nilai stasioner f(c) jika f '(c) = 0 dan titik (c, f(c)) disebut titik stasioner.

Contoh Soal 1 :

a. Tentukan nilai stasioner fungsi f(x) = 3x² – 6x + 5.

b. Tentukan nilai stasioner dan jenisnya untuk fungsi f(x) = x³ + 4x² – 3x + 2.

Pembahasan :

a. f(x) = 3x² – 6x + 5 → f '(x) =6x – 6

Nilai stasioner diperoleh jika f '(x) = 0 sehingga :

f '(x) = 0

6x – 6 = 0

x = 1.

f(1) = 3.1² – 6. 1 + 5 = 2

Jadi, nilai stasioner f(x) = 3x² – 6x + 5 adalah f(1) = 2

b. f(x) = x³ + 4x² – 3x + 2

f '(x) = 3x² + 8x – 3

untuk f '(x) = 0

3x² + 8x – 3 = 0

(3x – 1) (x + 3) = 0

x = 1/3 atau x = –3

↔ f ' (1/3) = 0 dan f '(–3) = 0

sehingga untuk x = 1/3 diperoleh :

untuk x = –3 diperoleh f(–3) = (–3)³ + 4 (3)² – 3.3 + 2 = 2

Jadi, nilai stasioner f(x) = x³ + 4x² – 3x + 2  adalah f (1/3) = 

dan f(–3) = 2.

Titik  dan (–3, 2) dinamakan titik stasioner.

Untuk menentukan jenis stasioner, pelajari interval f '(x) di bawah.

Untuk mengetahui nilai f '(x) pada selang x < –3, –3 < x < 1/3, dan x > 1/3, substitusikan nilai x untuk selang interval tersebut pada f '(x) sehingga diperoleh

• untuk x = –4, f '(–4) = 13 > 0 sehingga f(x) naik untuk x < –3;

• untuk x = 0, f '(0) = –3 < 0 sehingga f(x) turun untuk interval –3 < x < 1/3;

• untuk x = 1, f '(1) = 8 > 0 sehingga f(x) naik untuk x > 1/3.

Jadi, nilai f '(x) dapat digambarkan pada selang interval di atas.

Dari gambar untuk selang interval tersebut :

• titik (–3, 2) adalah titik maksimum,

• titik  adalah titik minimum.

2. Menentukan Nilai Stasioner Suatu Fungsi

Anda telah mempelajari cara menentukan nilai stasioner dengan uji tanda turunan pertama. Misalkan, fungsi f(x) = x³ – 3x² dengan f '(x) = 3x² – 6x. Untuk f '(x) = 0 diperoleh titik-titik stasioner (0, 0) dan (2, –4), dengan (0, 0) dinamakan titik balik maksimum lokal, sedangkan (2, –4) dinamakan titik balik minimum lokal. Sekarang, pelajarilah cara menentukan nilai stasioner suatu fungsi dan penerapannya menggunakan turunan kedua.

Dengan menggunakan turunan kedua jenis titik stasioner dapat ditentukan sebagai berikut.

• Jika f "(c) < 0, f(c) adalah nilai maksimum lokal fungsi f(x) dan titik (c, f(c)) adalah titik balik maksimum lokal grafik fungsi f(x).

• Jika f "(c) > 0, f(c) adalah nilai minimum lokal fungsi f(x) dan titik (c, f(c)) adalah titik balik minimum lokal grafik fungsi f(x).

• Jika f "(c) = 0 atau tidak mempunyai turunan kedua, jenis nilai stasioner dilakukan dengan menggunakan uji turunan pertama.

Contoh Soal 2 :

Tentukan jenis nilai stasioner fungsi f(x) = x³ – 6x² + 9x + 1 dan f(x) = x⁴ – 4x³ dengan menggunakan uji turunan kedua.

Penyelesaian :

• Untuk fungsi f(x) = x³ – 6x² + 9x + 1

f '(x) = 3x² – 12x + 9 = 3(x – 1) (x – 3)

f "(x) = 6x – 12

Nilai stasioner diperoleh untuk f '(x) = 0, yaitu :

3(x – 1) (x – 3) = 0

x = 1 atau x = 3

Nilai stasionernya adalah x = 1 atau x = 3 untuk x = 1, f "(1) = –6 < 0, sedangkan untuk x = 3, f "(3) = 6 > 0 sehingga :

f(1) adalah nilai maksimum lokal fungsi f(x), yaitu f(1) = 5

f(3) adalah nilai minimum lokal fungsi f(x), yaitu f(3) = 1

• Untuk fungsi f(x) = f(x) = x⁴ – 4x³

f '(x) = 4x³ – 12x² = 4x² (x – 3)

f "(x) = 12x² – 24x

Nilai stasioner diperoleh untuk f '(x) = 0, yaitu x = 0 atau x = 3 untuk x = 0, f "(0) = 0 dan untuk x = 3, f "(3) = 36 > 0 sehingga :

f(3) adalah nilai minimum lokal fungsi f(x), yaitu f(3) = –27.

Untuk x = 0 dengan f "(0) = 0 jenis nilai stasioner ditentukan dengan uji turunan pertama.

Sekarang, amati diagram di bawah ini.

Amati f "(x) > 0 untuk x < 0, dikatakan f cekung ke atas pada x < 0, f "(x) < 0 untuk 0 < x < 2, dikatakan f cekung ke bawah pada 0 < x < 2, dan f "(x) > 0 pada x > 2, dikatakan f cekung ke atas pada x > 2.

Di sekitar x = 0 (titik (0, 0)) terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah sehingga titik (0, 0) merupakan titik belok grafik fungsi f. Apakah titik (2, 0) merupakan titik belok? Bagaimana dengan titik (3, 0)?

Dari contoh tersebut dapatkah Anda menduga cara menentukan nilai stasioner suatu fungsi? Cobalah nyatakan dengan kata-kata Anda sendiri. Konsep yang telah Anda pelajari tersebut membawa kita pada definisi berikut.

Definisi 2 :

f cekung ke atas pada [a, b] jika f "(x) > 0 dan f cekung ke bawah jika f "(x) < 0. Perubahan kecekungan disebut titik belok.

Anda sekarang sudah mengetahui Nilai Stasioner Fungsi. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.

Referensi :

Djumanta, W. 2008. Mahir Mengembangkan Kemampuan Matematika 2 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 250.

Fungsi Naik dan Turun

Pertama, kita definisikan suatu fungsi dapat dikatakan sebagai fungsi naik atau fungsi turun. Perhatikan definisi berikut.

---

Definisi Fungsi Naik dan Turun

Suatu fungsi f dikatakan naik pada suatu selang jika untuk sembarang dua bilangan x1 dan x2 dalam selang tersebut, x1 < x2 mengakibatkan f(x1) < f(x2).

Suatu fungsi f dikatakan turun pada suatu selang jika untuk sembarang dua bilangan x1 dan x2 dalam selang tersebut, x1 < x2 mengakibatkan f(x1) > f(x2).

Suatu fungsi dikatakan naik jika x bergerak ke kanan, grafik fungsi tersebut bergerak ke atas, dan turun jika grafik fungsi tersebut bergerak ke bawah. Sebagai contoh, fungsi di samping naik pada selang (–∞, a), konstan pada selang (a, b), dan turun pada selang (b, ∞). Seperti yang ditunjukkan Teorema Uji Fungsi Naik dan Turun di bawah ini, turunan positif akan mengakibatkan suatu fungsi akan naik, turunan negatif akan mengakibatkan fungsi tersebut turun, dan turunan nol pada seluruh selang akan mengakibatkan fungsi tersebut konstan pada selang tersebut.

Teorema Uji Fungsi Naik dan Turun

Misalkan f adalah fungsi yang kontinu pada selang tutup [a, b] dan terdiferensialkan pada selang buka (a, b).

1. Jika f ’(x) > 0 untuk semua x dalam (a, b), maka f naik pada [a, b].
2. Jika f ’(x) < 0 untuk semua x dalam (a, b), maka f turun pada [a, b].
3. Jika f ’(x) = 0 untuk semua x dalam (a, b), maka f konstan pada [a, b].

---

Pembuktian

Kasus 1: Untuk membuktikan kasus pertama, anggap bahwa f ’(x) > 0 untuk semua x dalam selang (a, b) dan misalkan x1 < x2 adalah sembarang dua titik dalam selang tersebut. Berdasarkan Teorema Nilai Rata-Rata, kita tahu bahwa ada suatu bilangan c sedemikian sehingga x1 < c < x2, dan

Karena f ’(c) > 0 dan x2 – x1 > 0, maka f(x2) – f(x1) > 0, yang mengakibatkan bahwa f(x1) < f(x2). Jadi, f naik pada selang tersebut.

Kasus 2: Untuk kasus ini, kita dapat membuktikannya dengan menggunakan alur yang serupa dengan kasus 1.

Kasus 3: Misalkan f ’(x) = 0 untuk semua x dalam selang (a, b) dan misalkan x1 < x2 adalah sembarang duat titik dalam selang tersebut. Berdasarkan Teorema Nilai Rata-Rata, kita tahu bahwa ada suatu bilangan c sedemikian sehingga x1 < c < x2, dan

Karena f ’(c) = 0 maka f(x1) – f(x2) = 0, yang berakibat f(x1) = f(x2). Jadi, fungsi tersebut tidak naik ataupun tidak turun. Dengan kata lain, fungsi tersebut konstan pada selang tersebut.

Soal Nomor 1
Interval $x$ yang membuat kurva fungsi $f\left(x\right)=x^3-6x^2+9x+2$ selalu turun adalah $\cdots \cdot$
A. $-1<x<3$
B. $0<x<3$
C. $1<x<3$
D. $x<1$ atau $x>3$
E. $x<0$ atau $x>3$

Pembahasan

Diketahui $f\left(x\right)=x^3-6x^2+9x+2$

sehingga turunan pertamanya adalah $f^{\prime }\left(x\right)=3x^2-12x+9$.
Kurva $f\left(x\right)$ selalu turun jika diberi syarat $f^{\prime }\left(x\right)<0$.
$\begin{array}{cc}3x^2-12x+9& <0\\ \text{Kedua ruas dibagi}& \text{dengan}3\\ x^2-4x+3& <0\\ (x-3)(x-1)& <0\\ \therefore 1<x& <3\end{array}$
Jadi, interval $x$ yang membuat kurva fungsi $f\left(x\right)$ selalu turun adalah $1<x<3$
(Jawaban C)

Soal Nomor 2

Diberikan fungsi $g\left(x\right)=2x^3-9x^2+12x$. Interval $x$ yang memenuhi kurva fungsi $g\left(x\right)$ selalu naik adalah $\cdots \cdot$
A. $x<-2$ atau $x>-1$
B. $x<-1$ atau $x>2$
C. $x<1$ atau $x>2$
D. $1<x<2$
E. $-1<x<2$

Pembahasan

Diketahui $g\left(x\right)=2x^3-9x^2+12x$

, sehingga turunan pertamanya adalah $g^{\prime }\left(x\right)=6x^2-18x+12$.
Kurva $g\left(x\right)$ selalu naik jika diberi syarat $g^{\prime }\left(x\right)>0$.
$\begin{array}{cc}6x^2-18x+12& >0\\ \text{Kedua ruas dibagi}& \text{dengan}6\\ x^2-3x+2& >0\\ (x-2)(x-1)& >0\\ \therefore x<1\text{atau}x& >2\end{array}$ 

Jadi, interval $x$ yang membuat kurva fungsi $g\left(x\right)$ selalu naik adalah $x<1\text{atau}x>2$

(Jawaban C)

Soal Nomor 3
Grafik fungsi $p\left(x\right)=x(6-x{)}^2$

tidak pernah turun dalam interval $\cdots \cdot$
A. $x\le -2$ atau $x\ge 6$
B. $x\le 2$ atau $x\ge 6$
C. $x<2$ atau $x\ge 6$
D. $x\le 2$ atau $x>6$
E. $x<2$ atau $x>6$

Pembahasan

Diketahui $p\left(x\right)=x(6-x{)}^2$

. Turunan pertama $p\left(x\right)$ dapat dicari secara manual dengan menjabarkan seperti berikut (pangkatnya masih kecil, sehingga masih sangat memungkinkan untuk dijabarkan).
$\begin{array}{cc}p\left(x\right)& =x(6-x{)}^2\\ =x(36-12x+x^2)\\ =36x-12x^2+x^3\\ p^{\prime }\left(x\right)& =36-24x+3x^2\end{array}$ 

Grafik fungsi $p\left(x\right)$ tidak pernah turun jika diberi syarat $p^{\prime }\left(x\right)\ge 0$.
$\begin{array}{cc}36-24x+3x^2& \ge 0\\ \text{Kedua ruas dibagi}& \text{dengan}3\\ x^2-8x+12& \ge 0\\ (x-2)(x-6)& \ge 0\\ \therefore x\le 2\text{atau}x& \ge 6\end{array}$ 

Jadi, interval $x$ yang membuat grafik fungsi $p\left(x\right)$ tidak pernah turun adalah $x\le 2\text{atau}x\ge 6$

(Jawaban B)

Soal Nomor 4
Grafik fungsi $\pi \left(x\right)=x^3+3x^2+5$

tidak pernah naik untuk nilai-nilai $\cdots \cdot$
A. $-2\le x\le 0$
B. $-2\le x<0$
C. $-2<x\le 0$
D. $x\le -2$ atau $x\ge 0$
E. $-2<x<0$Pembahasan

Diketahui $\pi \left(x\right)=x^3+3x^2+5$

sehingga turunan pertamanya adalah ${\pi }^{\prime }\left(x\right)=3x^2+6x$.
Grafik fungsi $\pi \left(x\right)$ tidak pernah naik jika diberi syarat ${\pi }^{\prime }\left(x\right)\le 0$.

$\begin{array}{cc}3x^2+6x& \le 0\\ \text{Kedua ruas dibagi}& \text{dengan}3\\ x^2+2x& \le 0\\ x(x+2)& \le 0\\ \therefore -2\le x& \le 0\end{array}$ 

Jadi, interval $x$ yang membuat grafik fungsi $\pi \left(x\right)$ tidak pernah turun adalah $-2\le x\le 0$
(Jawaban A)

 Soal Nomor 5
Diberikan fungsi $R\left(x\right)=x^3-3x^2+3x-2$. Nilai-nilai $x$ dari fungsi tersebut mengakibatkan kurva fungsi $R\left(x\right)$ $\cdots \cdot$

A. tidak pernah naik
B. tidak pernah turun
C. bisa naik, bisa turun
D. selalu turun
E. selalu naik

Pembahasan

Diketahui $R\left(x\right)=x^3-3x^2+3x-2$

Turunan pertamanya adalah $R^{\prime }\left(x\right)=3x^2-6x+3$. Selanjutnya, kita akan mencari titik stasioner fungsi tersebut, yakni saat $R^{\prime }\left(x\right)=0$.
$\begin{array}{cc}3x^2-6x+3& =0\\ \text{Kedua ruas dibagi}& \text{dengan}3\\ x^2-2x+1& =0\\ (x-1{)}^2& =0\end{array}$ 

Perhatikan bahwa pada ekspresi $(x-1{)}^2$, kita mendapati bahwa nilai darinya tidak mungkin bertanda

 

negatif (ingat bahwa semua bilangan real yang dikuadratkan tidak akan bertanda negatif), sehingga grafik fungsi $R\left(x\right)$

tidak pernah turun, melainkan stasioner (tetap) atau naik, seperti yang tampak pada sketsa gambar berikut.

(Jawaban B)

Soal Nomor 6
Nilai-nilai $x$dari fungsi $y=\frac{x^2+3}{x-1}$ yang mengakibatkan kurva fungsi itu selalu turun adalah $\cdots \cdot$

A. $x<-1$ atau $x>3$
B. $-1<x<3$
C. $x<1$ atau $x>3$
D. $-1<x<1$ atau $1<x<3$
E. $-1<x<1$ atau $x>3$

Pembahasan

Diketahui $y=\frac{x^2+3}{x-1}$

Turunan pertamanya dapat ditentukan dengan menggunakan aturan hasil bagi.
Misalkan $u=x^2+3\Rightarrow u^{\prime }=2x$ dan $v=x-1\Rightarrow v^{\prime }=1$, sehingga
$\begin{array}{cc}{y}^{\prime }& =\frac{u^{\prime }v-u{v}^{\prime }}{v^2}\\ =\frac{2x(x-1)-(x^2+3)\left(1\right)}{(x-1{)}^2}\\ =\frac{2x^2-2x-x^2-3}{}\end{array}$

$\begin{array}{c}\frac{(x-1{)}^2}{}\\ =\frac{x^2-2x-3}{(x-1{)}^2}\\ =\frac{(x-3)(x+1)}{(x-1{)}^2}\end{array}$
Grafik fungsi tersebut selalu turun jika diberi syarat $y^{\prime }<0$, yaitu
$\frac{(x-3)(x+1)}{(x-1{)}^2}<0$.
Dari pertidaksamaan di atas, diketahui bahwa penyebut dipastikan bernilai positif untuk $x\ne 1$, sehingga yang memengaruhi tanda hanya pembilangnya saja.
Agar keseluruhan bernilai negatif, pembilangnya harus dibuat negatif.
$\begin{array}{cc}(x-3)(x+1)& <0\\ \therefore -1<x& <3\end{array}$
Karena $x\ne 1$ (berakibat penyebut bernilai $0$), maka kita peroleh bahwa interval $x$ yang memenuhi adalah seluruh bilangan di antara $-1$ dan $3$, kecuali $1$, kita tulis
$-1<x<1\text{atau}1<x<3$

(Jawaban D)

Soal Nomor 8
Grafik fungsi $f\left(x\right)=a{x}^3+x^2+5$

akan selalu naik dalam interval $0<x<2$. Nilai $a$ adalah $\cdots \cdot$
A. $-3$                     C. $\frac{1}{3}$                 E. $3$
B. $-\frac{1}{3}$                    D. $1$

Pembahasan

Diketahui $f\left(x\right)=a{x}^3+x^2+5$

dan $f\left(x\right)$ selalu naik di $0<x<2$, mengimplikasikan bahwa
$\begin{array}{cc}(x-0)(x-2)& <0\\ x(x-2)& <0\\ x^2-2x& <0& (\cdots 1)\end{array}$
Turunan pertama $f\left(x\right)$ adalah $f^{\prime }\left(x\right)=3a{x}^2+2x$.
Grafik fungsi $f\left(x\right)$ selalu naik jika diberi syarat $f^{\prime }\left(x\right)>0$.
$\begin{array}{cc}3a{x}^2+2x& >0\\ \text{Kedua ruas dikali}& \text{dengan}-1\\ -3a{x}^2-2x& <0& (\cdots 2)\end{array}$
Kaitkan pertidaksamaan $\left(1\right)$ dan $\left(2\right)$.
$\{\begin{array}{cc}{x}^2-2x& <0\\ -3a{x}^2-2x& <0\end{array}$
Diperoleh $-3a=1\Rightarrow a=-\frac{1}{3}$
Jadi, Nilai $a$ yang membuat $f\left(x\right)$ selalu naik pada interval tersebut adalah $-\frac{1}{3}$

(Jawaban B)

Soal Nomor 9
Grafik fungsi $T\left(x\right)=2x^3+3a{x}^2-4bx+5$ akan selalu turun dalam interval $-4<x<1$. Nilai $\frac{b}{a}$ adalah $\cdots \cdot$
A. $1$                    C. $3$                    E. $9$
B. $2$                    D. $6$Pembahasan

Diketahui $T\left(x\right)=2x^3+3a{x}^2-4bx+5$ dan $T\left(x\right)$ selalu turun di $-4<x<1$, mengimplikasikan bahwa
$\begin{array}{cc}(x+4)(x-1)& <0\\ x^2-x+4x-4& <0\\ x^2+3x-4& <0& (\cdots 1)\end{array}$
Turunan pertama $T\left(x\right)$ adalah $T^{\prime }\left(x\right)=6x^2+6ax-4b$.
Grafik fungsi $T\left(x\right)$ selalu turun jika diberi syarat $T^{\prime }\left(x\right)<0$.
$\begin{array}{cc}6x^2+6ax-4b& <0\\ \text{Kedua ruas dibagi}& \text{dengan}6\\ x^2+ax-\frac{2}{3}b& <0& (\cdots 2)\end{array}$
Kaitkan pertidaksamaan $\left(1\right)$ dan $\left(2\right)$.
$\{\begin{array}{cc}{x}^2+3x-4& <0\\ x^2+ax-\frac{2}{3}b& <0\end{array}$
Diperoleh:
$\begin{array}{cc}a& =3\left(✓\right)\\ \bullet -\frac{2}{3}b& =-4\Rightarrow b=6\left(✓\right)\end{array}$
Jadi, nilai $\frac{b}{a}=\frac{6}{3}=2$
(Jawaban B)

Soal Nomor 10
Grafik fungsi $f\left(x\right)=x^3+a{x}^2+bx+c$

hanya turun pada interval $-1<x<5$. Nilai $a+b=\cdots \cdot$
A. $-21$                  C. $-9$                   E. $21$
B. $-15$                  D. $9$

Pembahasan 

Diketahui $f\left(x\right)=x^3+a{x}^2+bx+c$

dan $f\left(x\right)$ selalu turun di $-1<x<5$, mengimplikasikan bahwa
$\begin{array}{cc}(x+1)(x-5)& <0\\ x^2-5x+x-5& <0\\ x^2-4x-5& <0& (\cdots 1)\end{array}$
Turunan pertama $f\left(x\right)$ adalah $f^{\prime }\left(x\right)=3x^2+2ax+b$.
Grafik fungsi $f\left(x\right)$ selalu turun jika diberi syarat $f^{\prime }\left(x\right)<0$.
$\begin{array}{cc}3x^2+2ax+b& <0\\ \text{Kedua ruas dibagi}& \text{dengan}3\\ x^2+\frac{2}{3}ax+\frac{1}{3}b& <0& (\cdots 2)\end{array}$

Kaitkan pertidaksamaan $\left(1\right)$ dan $\left(2\right)$.
$\{\begin{array}{cc}{x}^2-4x-5& <0\\ x^2+\frac{2}{3}ax+\frac{1}{3}b& <0\end{array}$
Diperoleh:
$\begin{array}{cc}\bullet \frac{2}{3}a& =-4\Rightarrow a=-6\\ \bullet \frac{1}{3}b& =-5\Rightarrow b=-15\end{array}$

Jadi, nilai $a+b=-6+(-15)=-21$

(Jawaban A)

Soal Nomor 11
Grafik fungsi $L\left(x\right)=a{x}^3+9b{x}^2-24x+5$

akan selalu naik dalam interval $x<-4$ atau $x>1$. Nilai $a+b$ adalah $\cdots \cdot$
A. $1$                    C. $3$                    E. $9$
B. $2$                    D. $6$

Pembahasan

Diketahui $L\left(x\right)=a{x}^3+9b{x}^2-24x+5$

dan $L\left(x\right)$ selalu naik di $x<-4$ atau $x>1$, mengimplikasikan bahwa
$\begin{array}{cc}(x+4)(x-1)& >0\\ x^2-x+4x-4& >0\\ x^2+3x-4& >0& (\cdots 1)\end{array}$
Turunan pertama $L\left(x\right)$ adalah $L^{\prime }\left(x\right)=3a{x}^2+18bx-24$.
Grafik fungsi $L\left(x\right)$ selalu naik jika diberi syarat $L^{\prime }\left(x\right)>0$.
$\begin{array}{cc}3a{x}^2+18bx-24& >0\\ \text{Kedua ruas dibagi}& \text{dengan}6\\ \frac{a}{2}{x}^2+3bx-4& >0& (\cdots 2)\end{array}$

Catatan: Mengapa harus dibagi 6? Karena kita harus membuat konstantanya menjadi $-4$ sesuai dengan pertidaksamaan $\left(1\right)$.
Berikutnya, kaitkan pertidaksamaan $\left(1\right)$ dan $\left(2\right)$.
$\{\begin{array}{cc}{x}^2+3x-4& >0\\ \frac{a}{2}{x}^2+3bx-4& >0\end{array}$
Diperoleh:
$\begin{array}{cc}\bullet \frac{a}{2}& =1\Rightarrow a=2\\ \bullet 3b& =3\Rightarrow b=1\end{array}$

Jadi, nilai $a+b=2+1=3$

(Jawaban C)

Soal Nomor 12
Fungsi $f\left(x\right)={\sin }^{2}x$

dengan $0<x<2\pi$ naik pada interval $\cdots \cdot$
A. $\frac{\pi }{2}<x<\pi$ atau $\frac{3\pi }{2}<x<2\pi$
B. $\frac{2\pi }{3}<x<\pi$
C. $0<x<\frac{\pi }{2}$ atau $\pi <x<\frac{3\pi }{2}$
D. $0<x<\pi$ atau $\pi <x<2\pi$
E. $0<x<2\pi$

Pembahasan

Diketahui $f\left(x\right)={\sin }^{2}x$

Turunan pertamanya adalah $f^{\prime }\left(x\right)=2\sin x\cos x=\sin 2x$. Grafik fungsi $f$ akan naik ketika diberi syarat $f^{\prime }\left(x\right)>0$, yaitu $\sin 2x>0$.
Pembuat nol adalah $\{0,\frac{\pi }{2},\pi ,\frac{3\pi }{2},2\pi \}$.
Buat garis bilangan dan tentukan tanda kepositivan dengan uji titik.

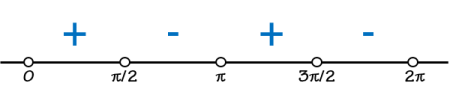
Ini berarti, $\sin 2x>0$ terpenuhi ketika $0<x<\frac{\pi }{2}$ atau $\pi <x<\frac{3\pi }{2}$. Jadi, $f\left(x\right)={\sin }^{2}x$ akan naik pada interval $0<x<\frac{\pi }{2}$ atau $\pi <x<\frac{3\pi }{2}$

, seperti yang dipertegas pada sketsa grafik berikut.
(Jawaban C)

 

DAFTAR PUSTAKA

https://yos3prens.wordpress.com/2015/03/24/penerapan-turunan-fungsi-naik-dan-turun-serta-uji-turunan-pertama/#:~:text=Definisi%20Fungsi%20Naik%20dan%20Turun&text=Suatu%20fungsi%20dikatakan%20naik%20jika,selang%20(b%2C%20%E2%88%9E).

https://www.nafiun.com/2014/06/pengertian-nilai-stasioner-fungsi-contoh-soal-rumus-cara-menetukan-dan-menghitung-pembahasan-matematika.html